题目内容
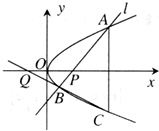 如图,已知抛物线y2=2px(p>0)上纵坐标为1的点到焦点的距离为p,过点P(1,0)做斜率为k的直线l交抛物线于A,B两点,A点关于x轴的对称点为C,直线BC交x轴于Q点;
如图,已知抛物线y2=2px(p>0)上纵坐标为1的点到焦点的距离为p,过点P(1,0)做斜率为k的直线l交抛物线于A,B两点,A点关于x轴的对称点为C,直线BC交x轴于Q点;(1)求p的值;
(2)求证:点Q是定点,并求出点Q的坐标.
分析:(1)设抛物线y2=2px(p>0)上纵坐标为1的点为M,则M(
,1),利用抛物线的定义得出其到焦点的距离等于到准线的距离,列出关于p的方程求解即可;
(2)由(1)得:抛物线方程为:y2=2x,设过点P(1,0)做斜率为k的直线l的方程为:y=k(x-1),将直线的方程代入抛物线的方程,消去x得到关于y的一元二次方程,再结合根与系数的关系利用直线的主程即可求得求出点Q的坐标,从而解决问题.
| 1 |
| 2p |
(2)由(1)得:抛物线方程为:y2=2x,设过点P(1,0)做斜率为k的直线l的方程为:y=k(x-1),将直线的方程代入抛物线的方程,消去x得到关于y的一元二次方程,再结合根与系数的关系利用直线的主程即可求得求出点Q的坐标,从而解决问题.
解答:解:(1)设抛物线y2=2px(p>0)上纵坐标为1的点为M,则M(
,1),
其到焦点的距离等于到准线的距离,即
+
=p,∴p=1.
(2)由(1)得:抛物线方程为:y2=2x,
设过点P(1,0)做斜率为k的直线l的方程为:y=k(x-1)代入抛物线方程得:
y2=2(1+
),即y2-2
-2=0,设点A(xA,yA),B(xB,yB)
则yAyB=-2,
A点关于x轴的对称点为C(xA,-yA),
直线BC的方程为:y-yB=
(x-xB),令y=0得:
x=xB+
×(-yB)=xB+
×(-yB)=xB+
×(-yB2+yAyB)
=
×yAyB
=-1,
即点Q是定点,点Q的坐标(-1,0).
| 1 |
| 2p |
其到焦点的距离等于到准线的距离,即
| 1 |
| 2p |
| p |
| 2 |
(2)由(1)得:抛物线方程为:y2=2x,
设过点P(1,0)做斜率为k的直线l的方程为:y=k(x-1)代入抛物线方程得:
y2=2(1+
| y |
| k |
| y |
| k |
则yAyB=-2,
A点关于x轴的对称点为C(xA,-yA),
直线BC的方程为:y-yB=
| y B+y A |
| x B-x A |
x=xB+
| x B-x A |
| y B+y A |
| ||||
| y B+y A |
| 1 |
| 2p |
=
| 1 |
| 2p |
=-1,
即点Q是定点,点Q的坐标(-1,0).
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到抛物线的定义、轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
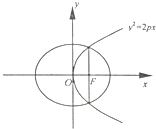 如图,已知抛物线y2=2px(p>0)的焦点恰好是椭圆
如图,已知抛物线y2=2px(p>0)的焦点恰好是椭圆| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、2(
| ||||
C、
| ||||
D、
|
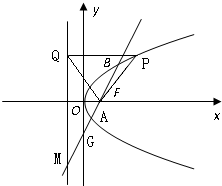 如图,已知抛物线y2=2px(p>0),焦点为F,准线为直线l,P为抛物线上的一点,过点P作l的垂线,垂足为点Q.当P的横坐标为3时,△PQF为等边三角形.
如图,已知抛物线y2=2px(p>0),焦点为F,准线为直线l,P为抛物线上的一点,过点P作l的垂线,垂足为点Q.当P的横坐标为3时,△PQF为等边三角形. 过抛物线焦点垂直于对称轴的弦叫做抛物线的通径.如图,已知抛物线y2=2px(p>0),过其焦点F的直线交抛物线于A(x1,y1)、B(x2,y2)两点,过A、B作准线的垂线,垂足分别为A1、B1.
过抛物线焦点垂直于对称轴的弦叫做抛物线的通径.如图,已知抛物线y2=2px(p>0),过其焦点F的直线交抛物线于A(x1,y1)、B(x2,y2)两点,过A、B作准线的垂线,垂足分别为A1、B1. (2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,….
(2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,…. 如图,已知抛物线y2=2px(p>0),过它的焦点F的直线l与其相交于A,B两点,O为坐标原点.
如图,已知抛物线y2=2px(p>0),过它的焦点F的直线l与其相交于A,B两点,O为坐标原点.