题目内容

已知函数f(x)=px3+qx+k是定义在R上的奇函数，且f(1)=数f(x)的极值．

(Ⅰ)求函数f(x)的表达式；

(Ⅱ)在y=f(x)的曲线上是否存在不同的两个整点M、N，使得过M点的切线与过N点的切线平行，且它们与直线MN的夹角为45°．若存在，求出M、N的坐标；若不存在，请说明理由．

解：(Ⅰ)∵f(x)是定义在R上的奇函数．

∴f(0)=0  k=0．

又f′(x)=3px2+q  且f(1)=-1是函数的极值．

∴即解之得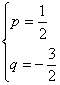

∴f(x)=x3-x

(Ⅱ)设M(xl，y1)，N(x2，y2)．(x1≠x2)

∵f′(x)=x2-．

∴过M、N的切线斜率分别为

k1=

由题意知k1=k2  ∴

但x1≠x2   ∴x1=-x2，从而y1=-y2

直线MN的斜率k3=

∵过M的直线与MN夹角为45°

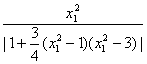∴=1

化简得  3+13=0或3=0

由3+13=0得△＜0  ∴方程无解

由3=0得或=

∴x1=±1或x1=± (舍去)

∴M(1，-1)，N(-1，1)或M(-1，1)，N(1，-1).


练习册系列答案
相关题目
已知函数f(x)=
1
2
x2-alnx的图象在点P（2，f（2））处的切线方程为l：y=x+b
（1）求出函数y=f（x）的表达式和切线l的方程；
（2）当x∈[
1
e
，e]时（其中e=2.71828…），不等式f（x）＜k恒成立，求实数k的取值范围．
已知函数f(x)=
-x3+x2+bx+c
 ，(x＜1)
alnx
 ，(x≥1)
的图象过坐标原点O，且在点（-1，f（-1））处的切线的斜率是-5．
（1）试确定实数b，c的值，并求f（x）在区间[-1，2]上的最大值；
（2）对任意给定的正实数a，曲线y=f（x）上是否存在两点P、Q，使得△POQ是以O为直角顶点的直角三角形，且此三角形斜边中点在y轴上？说明理由．
已知函数f(x)=lnx，g(x)=
1
2
ax2+bx(a≠0)，h(x)=
2(x-1)
x+1

（1）当a=-2时，函数F（x）=f（x）-g（x）在其定义域范围是增函数，求实数b的取值范围；
（2）当x＞1时，证明f（x）＞h（x）成立；
（3）记函数f（x）与g（x）的图象分别是C1、C2，C1、C2相交于不同的两点P，Q，过线段PQ的中点R作垂直于x轴的垂线，与C1、C2分别交于M、N，问是否存在点R，使得曲线C1在M处的切线与曲线C2在N处的切线平行？若存在，试求出R点的坐标；若不存在，试说明理由．
已知函数f(x)=x+
tx
(x＞0)，过点P（1，0）作曲线y=f（x）的两条切线PM，PN，切点分别为M，N．
（1）当t=2时，求函数f（x）的单调递增区间；
（2）设|MN|=g（t），试求函数g（t）的表达式．
已知函数f(x)=log3
3
x
1-x
，M(x1，y1)，N(x2，y2)是f（x）图象上的两点，横坐标为
1
2
的点P满足2
OP
=
OM
+
ON
（O为坐标原点）．
（1）求证：y1+y2为定值；
（2）若Sn=f(
1
n
)+f(
2
n
)+…+f(
n-1
n
)，其中n∈N*，n≥2令an=
1
6
，n=1
1
4(Sn+1)(Sn+1+1)
，n≥2
，其中n∈N*，Tn为数列{an}的前n项和，若Tn＜m（Sn+1+1）对一切n∈N*都成立，试求m的取值范围．
（3）对于给定的实数a（a＞1）是否存在这样的数列{an}，使得f(an)=log3(
3
an+1)，且a1=
1
a-1
？若存在，求出a满足的条件；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网