题目内容
已知圆x2+y2-2y=0上任一点p(x,y)
(1)求2x+y的取值范围
(2)若x+y+c≥0恒成立,求实数c的最小值.
解:(1)由圆x2+y2-2y=0可化为x2+(y-1)2=1,圆心为C(0,1),半径r=1.
设2x+y=t,则y=-2x+t.
∵直线y=-2x+t与圆有公共点,∴圆心C(0,1)到直线的距离d= ,解得
,解得 .
.
因此2x+y的取值范围是 .
.
(2)点p(x,y)在圆上,x+y+c≥0恒成立?c≥[-(x+y)]max,点p(x,y)满足圆的方程.
设s=-(x+y),则y=-x-s,∵点p(x,y)在圆上,
∴圆心C(0,1)到直线的距离d≤r,即 ,解得
,解得 ,
,
∴s的最大值为 ,因此c
,因此c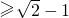 .
.
故c的最小值为 .
.
分析:(1)设2x+y=t,由于点p(x,y)在圆上,因此求2x+y的取值范围?圆心C到直线的距离d≤r,利用点到直线的距离求出即可;
(2)由于点p(x,y)在圆上,因此x+y+c≥0恒成立?c≥[-(x+y)]max,点p(x,y)满足圆的方程.设s=-(x+y),则利用点到直线的距离求出圆心到直线的距离d≤r,解出即可.
点评:正确把求取值范围转化为圆心到直线的距离d≤r是解题的关键.
设2x+y=t,则y=-2x+t.
∵直线y=-2x+t与圆有公共点,∴圆心C(0,1)到直线的距离d=
 ,解得
,解得 .
.因此2x+y的取值范围是
 .
.(2)点p(x,y)在圆上,x+y+c≥0恒成立?c≥[-(x+y)]max,点p(x,y)满足圆的方程.
设s=-(x+y),则y=-x-s,∵点p(x,y)在圆上,
∴圆心C(0,1)到直线的距离d≤r,即
 ,解得
,解得 ,
,∴s的最大值为
 ,因此c
,因此c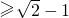 .
.故c的最小值为
 .
.分析:(1)设2x+y=t,由于点p(x,y)在圆上,因此求2x+y的取值范围?圆心C到直线的距离d≤r,利用点到直线的距离求出即可;
(2)由于点p(x,y)在圆上,因此x+y+c≥0恒成立?c≥[-(x+y)]max,点p(x,y)满足圆的方程.设s=-(x+y),则利用点到直线的距离求出圆心到直线的距离d≤r,解出即可.
点评:正确把求取值范围转化为圆心到直线的距离d≤r是解题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目


