题目内容
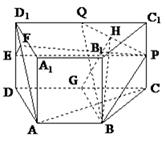
如图,直四棱柱ABCD-A1B1C1D1的底面是
梯形,AB∥CD,AD⊥DC,CD=2,DD1=AB=1,P、Q分别是CC1、C1D1的中点。点P到直线
AD1的距离为![]()
⑴求证:AC∥平面BPQ
⑵求二面角B-PQ-D的大小

(Ⅰ)证明见解析(Ⅱ)arctan![]()
解析:
⑴连接CD1 ∵P、Q分别是CC1、C1D1的
中点。∴CD1∥PQ 故CD1∥平面BPQ
 又D1Q=AB=1,D1Q∥AB,
又D1Q=AB=1,D1Q∥AB,
得平行四边形ABQD1,故AD1∥平面BPQ
∴平面ACD1∥平面BPQ
∴AC∥平面BPQ (4分)
⑵设DD1中点为E,连EF,则PE∥CD
∵CD⊥AD,CD⊥DD1 ∴CD⊥平面ADD1
∴PE⊥平面ADD1
过E作EF⊥AD1于F,连PF。则PF⊥AD1,PF为点P到直线AD1的距离
PF=![]() ,PE=2 ∴EF=
,PE=2 ∴EF=![]() 又D1E=
又D1E=![]() ,D1D=1,∴AD=1
,D1D=1,∴AD=1
取CD中点G,连BG,由AB∥DG,AB=DG得GB∥AD。∵AD⊥DC,AD⊥DD1∴AD⊥平面DCC1D1,则BG⊥平面DCC1D1
过G作GH⊥PQ于H,连BH,则BH⊥PQ,故∠BHG是二面角B-PQ-D的平面角。
由△GHQ∽△QC1P得GH=![]() ,又BG=1,得tan∠BHG=
,又BG=1,得tan∠BHG=![]()
∴二面角B-PQ-D大小为arctan![]()

练习册系列答案
相关题目
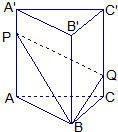 如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为
如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2. 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8. (2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.
(2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.