题目内容
给出下列四个命题:
①函数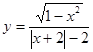 为奇函数;
为奇函数;
②奇函数的图像一定通过直角坐标系的原点;
③函数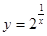 的值域是
的值域是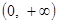 ;
;
④若函数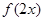 的定义域为
的定义域为 ,则函数
,则函数 的定义域为
的定义域为 ;
;
⑤函数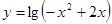 的单调递增区间是
的单调递增区间是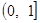 .
.
其中正确命题的序号是 .(填上所有正确命题的序号)
①函数
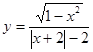 为奇函数;
为奇函数;②奇函数的图像一定通过直角坐标系的原点;
③函数
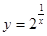 的值域是
的值域是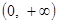 ;
;④若函数
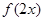 的定义域为
的定义域为 ,则函数
,则函数 的定义域为
的定义域为 ;
;⑤函数
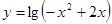 的单调递增区间是
的单调递增区间是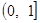 .
.其中正确命题的序号是 .(填上所有正确命题的序号)
①④⑤
试题分析:命题①中函数可化为
 ,易知此函数为奇函数,故命题①正确;命题②中比如函数
,易知此函数为奇函数,故命题①正确;命题②中比如函数 为奇函数,但其图像末经过原点,故命题②错;命题③中由于
为奇函数,但其图像末经过原点,故命题②错;命题③中由于 ,所以函数
,所以函数 ,即函数的值域应为
,即函数的值域应为 ,故命题③错;命题④中由函数
,故命题③错;命题④中由函数 的定义域为
的定义域为 ,则有
,则有 ,所以有
,所以有 ,解得
,解得 ,故命题④正确;命题⑤中由于函数
,故命题④正确;命题⑤中由于函数 为增函数,函数
为增函数,函数 在区间
在区间 上为单调递增函数,所以若函数
上为单调递增函数,所以若函数 为单调递增,则
为单调递增,则 ,解得
,解得 ,故命题⑤正确.所以正确答案为①④⑤.
,故命题⑤正确.所以正确答案为①④⑤.
练习册系列答案
相关题目
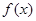 的图象经过点
的图象经过点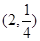 .
.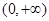 上的单调性,并用单调性的定义证明.
上的单调性,并用单调性的定义证明.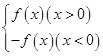
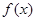 满足
满足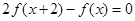 ,当
,当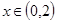 时,
时,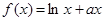
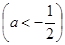 ,当
,当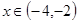 时,
时, 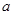 的值;
的值;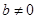 ,函数
,函数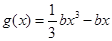 ,
,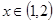 .若对任意的
.若对任意的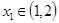 ,总存在
,总存在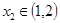 ,使
,使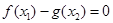 ,求实数
,求实数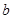 的取值范围.
的取值范围. 的定义域为
的定义域为 ,且对其内任意实数
,且对其内任意实数 均有:
均有: ,则
,则
 在
在 上是减函数,则实数
上是减函数,则实数 的取值范围是________.
的取值范围是________. ,
, 满足
满足 ,则
,则 的最小值为___.
的最小值为___.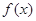 同时满足以下三个条件时称
同时满足以下三个条件时称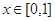 ,总有
,总有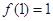 ;
; 成立,则下列判断正确的有 .
成立,则下列判断正确的有 .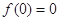 ;
;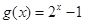 在区间[0,1]上是“友谊函数”;
在区间[0,1]上是“友谊函数”;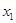 <
<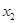 ≤1,则
≤1,则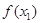 ≤
≤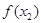 .
.  满足
满足 ,且不等式
,且不等式 在
在 上恒成立,则函数
上恒成立,则函数 =
= 的零点的个数为( )
的零点的个数为( )