题目内容
已知等比数列{an}中,a1=3,a4=81,若数列{bn}满足bn=log3an,则数列 的前n项和Sn= .
的前n项和Sn= .
【答案】分析:根据q3=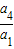 求得q,进而根据等比数列的通项公式求得an,则bn可得,最后利用裂项法求得数列
求得q,进而根据等比数列的通项公式求得an,则bn可得,最后利用裂项法求得数列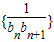 的前n项的和.
的前n项的和.
解答:解:q3=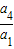 =27,求得q=3
=27,求得q=3
∴an=3×3n-1=3n,
∴bn=log3an=n,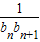 =
=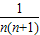 =
=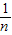 -
-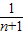
∴Sn=1- +
+ -
- +…+
+…+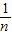 -
-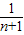 =1-
=1-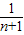 =
=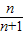
故答案为: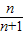
点评:本题主要考查了等比数列的性质.考查了学生对基础知识的综合运用.
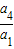 求得q,进而根据等比数列的通项公式求得an,则bn可得,最后利用裂项法求得数列
求得q,进而根据等比数列的通项公式求得an,则bn可得,最后利用裂项法求得数列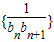 的前n项的和.
的前n项的和.解答:解:q3=
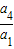 =27,求得q=3
=27,求得q=3∴an=3×3n-1=3n,
∴bn=log3an=n,
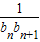 =
=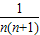 =
=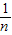 -
-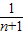
∴Sn=1-
 +
+ -
- +…+
+…+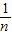 -
-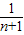 =1-
=1-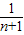 =
=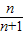
故答案为:
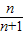
点评:本题主要考查了等比数列的性质.考查了学生对基础知识的综合运用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目