题目内容
【题目】如图,在平面直角坐标系xoy中,已知椭圆C: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E. 
(1)求椭圆C的方程;
(2)已知P为AD的中点,是否存在定点Q,对于任意的k(k≠0)都有OP⊥EQ,若存在,求出点Q的坐标;若不存在说明理由;
(3)若过O点作直线l的平行线交椭圆C于点M,求 ![]() 的最小值.
的最小值.
【答案】
(1)解:∵椭圆C: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,左顶点为A(﹣4,0),
,左顶点为A(﹣4,0),
∴a=4,又 ![]() ,∴c=2.…(2分)
,∴c=2.…(2分)
又∵b2=a2﹣c2=12,
∴椭圆C的标准方程为 ![]() .
.
(2)解:直线l的方程为y=k(x+4),
由 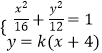 消元得,
消元得, ![]() .
.
化简得,(x+4)[(4k2+3)x+16k2﹣12)]=0,
∴x1=﹣4, ![]() .…(6分)
.…(6分)
当 ![]() 时,
时, ![]() ,
,
∴ ![]() .
.
∵点P为AD的中点,∴P的坐标为 ![]() ,
,
则 ![]() .…(8分)
.…(8分)
直线l的方程为y=k(x+4),令x=0,得E点坐标为(0,4k),
假设存在定点Q(m,n)(m≠0),使得OP⊥EQ,
则kOPkEQ=﹣1,即 ![]() 恒成立,
恒成立,
∴(4m+12)k﹣3n=0恒成立,∴ ![]() ,即
,即 ![]() ,
,
∴定点Q的坐标为(﹣3,0).
(3)解:∵OM∥l,∴OM的方程可设为y=kx,
由 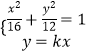 ,得M点的横坐标为
,得M点的横坐标为 ![]() ,
,
由OM∥l,得 ![]()
= 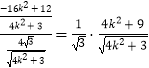
= ![]() ,
,
当且仅当 ![]() 即
即 ![]() 时取等号,
时取等号,
∴当 ![]() 时,
时, ![]() 的最小值为
的最小值为 ![]() .
.
【解析】(1)由椭圆的离心率和左顶点,求出a,b,由此能求出椭圆C的标准方程.(2)直线l的方程为y=k(x+4),与椭圆联立,得,(x+4)[(4k2+3)x+16k2﹣12)]=0,由此利用韦达定理、直线垂直,结合题意能求出结果.(3)OM的方程可设为y=kx,与椭圆联立得M点的横坐标为 ![]() ,由OM∥l,能求出结果.
,由OM∥l,能求出结果.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案