题目内容
已知函数f(x)在区间[0,π]上单调递减,且f(x)的图象关于y轴对称,f(-3),f( ),f(
),f( )的大小关系为
)的大小关系为
- A.f(
 )<f(
)<f( )<f(-3)
)<f(-3) - B.f(
 )<f(-3)<f(
)<f(-3)<f( )
) - C.f(-3)<f(
 )<f(
)<f( )
) - D.f(-3)<f(
 )<f(
)<f( )
)
C
分析:由f(x)的图象关于y轴对称知f(x)的奇偶性,则f(-3)=f(3),根据函数的单调性及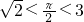 ,知f(
,知f( )>f(
)>f( )>f(3)=f(-3),从而得到答案.
)>f(3)=f(-3),从而得到答案.
解答:由f(x)的图象关于y轴对称知,f(x)为偶函数,
所以f(-3)=f(3),
因为f(x)在区间[0,π]上单调递减,且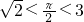 ,
,
所以f( )>f(
)>f( )>f(3)=f(-3),
)>f(3)=f(-3),
故选C.
点评:本题考查函数的奇偶性、单调性的综合及其应用,属中档题.
分析:由f(x)的图象关于y轴对称知f(x)的奇偶性,则f(-3)=f(3),根据函数的单调性及
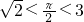 ,知f(
,知f( )>f(
)>f( )>f(3)=f(-3),从而得到答案.
)>f(3)=f(-3),从而得到答案.解答:由f(x)的图象关于y轴对称知,f(x)为偶函数,
所以f(-3)=f(3),
因为f(x)在区间[0,π]上单调递减,且
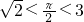 ,
,所以f(
 )>f(
)>f( )>f(3)=f(-3),
)>f(3)=f(-3),故选C.
点评:本题考查函数的奇偶性、单调性的综合及其应用,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目