Question

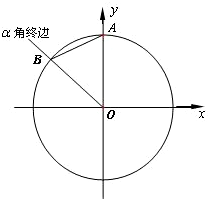（2011•福建模拟）如图，单位圆（半径为1的圆）的圆心O为坐标原点，单位圆与y轴的正半轴交与点A，与钝角α的终边OB交于点B（x_B，y_B），设∠BAO=β．
（1）用β表示α； 
（2）如果sinβ=

4

5

，求点B（x_B，y_B）的坐标；
（3）求x_B-y_B的最小值．

Answer 1

分析：（1）作出图形，结合图形由∠AOB=α-

π

2

=π-2β，能求出α=

3π

2

-2β．
（2）由sinα=

yB

r

，r=1，得yB=sinα=sin(

3π

2

-2β)=-cos2β=2sin2β-1=2•(

4

5

)2-1=

7

25

．由此能求出点B（x_B，y_B）的坐标；
（3）【法一】xB-yB=cosα-sinα=

2

cos(α+

π

4

)，由此能求出x_B-y_B的最小值．
【法二】由α为钝角，知x_B＜0，y_B＞0，x_B²+y_B²=1，x_B-y_B=-（-x_B+y_B），（-x_B+y_B）²≤2（x_B²+y_B²）=2，由此能求出x_B-y_B的最小值．

解答：解：（1）如图，∵∠AOB=α-

π

2

=π-2β，
∴α=

3π

2

-2β．4分
（2）由sinα=

yB

r

，又r=1，
得yB=sinα=sin(

3π

2

-2β)
=-cos2β=2sin2β-1=2•(

4

5

)2-1=

7

25

．7分
由钝角α，
知xB=cosα=-

1-sin2α

=-

24

25

，
∴B(-

24

25

，

7

25

).9分
（3）【法一】xB-yB=cosα-sinα=

2

cos(α+

π

4

)，
又α∈(

π

2

，π)，α+

π

4

∈(

3π

4

，

5π

4

)，
cos(α+

π

4

)∈[-1，-

2

2

)，
∴x_B-y_B的最小值为-

2

13分
【法二】α为钝角，
∴x_B＜0，y_B＞0，
x_B²+y_B²=1，
x_B-y_B=-（-x_B+y_B），
（-x_B+y_B）²≤2（x_B²+y_B²）=2，
∴xB-yB≥-

2

，
∴x_B-y_B的最小值为-

2

．13分

点评：本题考查三角函数的性质和应用，综合性强，是高考的常见题型．解题时要认真审题，仔细解答，注意三角函数恒等变换的灵活运用．