题目内容
以下三个命题:①关于x的不等式
≥1的解为(-∞,1]②曲线y=2sin2x与直线x=0,x=
及x轴围成的图形面积为s1,曲线y=
与直线x=0,x=2及x轴围成的图形面积为s2,则s1+s2=2③直线x-3y=0总在函数y=lnx图象的上方其中真命题的个数是( )
| 1 |
| x |
| 3π |
| 4 |
| 1 |
| π |
| 4-x2 |
| A.0 | B.1 | C.2 | D.3 |
①不等式
≥1等价于
≥0,∴0<x≤1,故错误;
②s1=3∫
2sin2xdx=3(-cos2x)|
=3,s2=
dx=4,∴s1+s2=7,故错误;
③构造函数f(x)=lnx-
,∴f /(x)=
-
∴x=3时,函数取得极大值且大于0,从而可知函数f(x)=lnx-
值有正也有负,所以直线x-3y=0不总在函数y=lnx图象的上方,故错误
故选A.
| 1 |
| x |
| 1-x |
| x |
②s1=3∫
|
|
| ∫ | 20 |
| 1 |
| π |
| 4-x2 |
③构造函数f(x)=lnx-
| x |
| 3 |
| 1 |
| x |
| 1 |
| 3 |
| x |
| 3 |
故选A.

练习册系列答案
相关题目
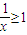 的解为(-∞,1]②曲线y=2sin2x与直线x=0,
的解为(-∞,1]②曲线y=2sin2x与直线x=0,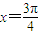 及x轴围成的图形面积为s1,曲线
及x轴围成的图形面积为s1,曲线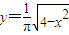 与直线x=0,x=2及x轴围成的图形面积为s2,则s1+s2=2③直线x-3y=0总在函数y=lnx图象的上方其中真命题的个数是( )
与直线x=0,x=2及x轴围成的图形面积为s2,则s1+s2=2③直线x-3y=0总在函数y=lnx图象的上方其中真命题的个数是( )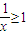 的解为(-∞,1]②曲线y=2sin2x与直线x=0,
的解为(-∞,1]②曲线y=2sin2x与直线x=0,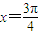 及x轴围成的图形面积为s1,曲线
及x轴围成的图形面积为s1,曲线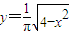 与直线x=0,x=2及x轴围成的图形面积为s2,则s1+s2=2③直线x-3y=0总在函数y=lnx图象的上方其中真命题的个数是( )
与直线x=0,x=2及x轴围成的图形面积为s2,则s1+s2=2③直线x-3y=0总在函数y=lnx图象的上方其中真命题的个数是( )