题目内容
设（2x-1）10=a+a1x+a2x2+…+a10x10，则a1+a3+a5+a7+a9的值（ ）A．
B．
C．
D．-
【答案】分析：通过对x赋值1得各项系数和，通过对x赋值-1得正负号交替的各项系数和，把所得的两个式子相减，得到下标是奇数的项的系数和的2倍，得到结果．
解答：解：令展开式的x=1得a+a1+a2+…+a9+a10=1
令x=-1得a-a1+a2+…-a9+a10=310
两式相减得：1-310=2（a1+a3+a5+a7+a9）
∴a1+a3+a5+a7+a9=
．
故选：B．
点评：本题考查求展开式的有关系数和问题的重要方法是赋值法，本题解题的关键是看出给变量赋值以后，两个式子相减，得到要求的结果的2倍．
解答：解：令展开式的x=1得a+a1+a2+…+a9+a10=1
令x=-1得a-a1+a2+…-a9+a10=310
两式相减得：1-310=2（a1+a3+a5+a7+a9）
∴a1+a3+a5+a7+a9=
．故选：B．
点评：本题考查求展开式的有关系数和问题的重要方法是赋值法，本题解题的关键是看出给变量赋值以后，两个式子相减，得到要求的结果的2倍．
练习册系列答案
考前必练系列答案
相关题目
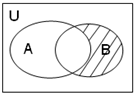设A={x|1≤x≤10，x∈N}，B={x|x2+2x-8=0，x∈R}，全集U=R，则图中阴影表示的集合中的元素为
