题目内容
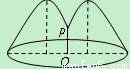
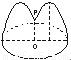
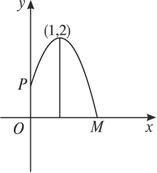
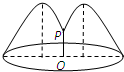如图，花坛水池中央有一喷泉，水管OP=1m，水从喷头P喷出后呈抛物线状先向上至最高点后落下，若最高点距水面2m，P距抛物线对称轴1m，则在水池直径的下列可选值中，最合算的是（ ）| A、2.5m | B、4m | C、5m | D、6m |
分析：建立直角坐标系，借助坐标法先求出落点的最远距离，从而估算出水池直径即可．
解答：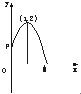
解：以O为原点，OP所在直线为y轴建立直角坐标系（如图），则抛物线方程可设为
y=a（x-1）2+2，P点坐标为（0，1），
∴1=a+2．∴a=-1．
∴y=-（x-1）2+2．
令y=0，得（x-1）2=2，∴x=1±
．
∴水池半径OM=
+1≈2.414（m）．
因此水池直径约为2×|OM|=4.828（m）．
解：以O为原点，OP所在直线为y轴建立直角坐标系（如图），则抛物线方程可设为y=a（x-1）2+2，P点坐标为（0，1），
∴1=a+2．∴a=-1．
∴y=-（x-1）2+2．
令y=0，得（x-1）2=2，∴x=1±
| 2 |
∴水池半径OM=
| 2 |
因此水池直径约为2×|OM|=4.828（m）．
点评：解决实际问题通常有几个步骤：（1）阅读理解，认真审题；（2）引进数学符号，建立数学模型，其中关键是建立数学模型．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
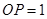米，水从喷头
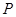喷出后呈抛物线状，先向上至最高点后落下，如果最高点距离水面2米，
