题目内容
数列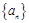
中，a1，a2－a1，a3－a2，，an－an－1是首项为1、公比为
的等比数列，则an等于( )
A． | B． | C． | D． |
D
解析试题分析：由题意得：
将这
个式子相加得：
选D.
考点：叠加法求通项
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
设数列
满足
，
，
，则数列的前n项和可以表示为（ ）
A． | B． | C． | D． |
在△ABC中, 
所对的边分别为
，若
则
等于 （ ）
A． | B． | C． | D． |
, 则数列{
}的前5项和为（ ）
等比数列
中,
前三项和为S3＝27，则公比q的值是( )
| A．1 | B．－ | C．1或－ | D．－1或－ |
已知等比数列
的前
项和为
，且
，
，
成等差数列，则数列的公比为( )
| A．1 | B．2 | C． | D．3 |
已知等比数列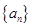
的前
项和为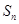
,则下列一定成立的是( )
A．若 ,则 | B．若 ,则 |
C．若,则 | D．若.则 |
已知数列
是无穷等比数列，其前n项和是
，若
，
，则
的值为 ( )
A． | B． | C． | D． |
的左．右顶点分别是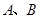
，左．右焦点分别是
，若
成等比数列，则此椭圆的离心率为（ ）
