题目内容
在空间直角坐标系O-xyz中,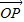 =
=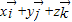 (其中
(其中 分别为x轴、y轴、z轴正方向上的单位向量).有下列命题:
分别为x轴、y轴、z轴正方向上的单位向量).有下列命题:①若
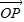 =
=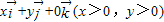 且|
且|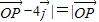
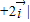 ,则
,则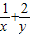 的最小值为2
的最小值为2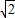
②若

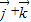 ,若向量
,若向量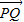 与
与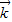 共线且|
共线且|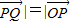 |,则动点P的轨迹是抛物线;
|,则动点P的轨迹是抛物线;③若
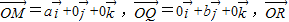 =
=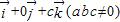 ,则平面MQR内的任意一点A(x,y,z)的坐标必须满足关系式
,则平面MQR内的任意一点A(x,y,z)的坐标必须满足关系式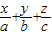 =1;
=1;④设
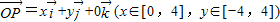 ,
,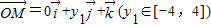 ,
,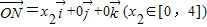 ,若向量
,若向量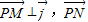 与
与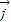 共线且|
共线且|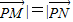 |,则动点P的轨迹是双曲线的一部分.
|,则动点P的轨迹是双曲线的一部分.其中你认为正确的所有命题的序号为 .
【答案】分析:命题①利用|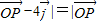
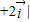 得到两个正数x,y的关系
得到两个正数x,y的关系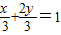 ,求
,求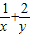 的最小值时只要把“1”代入展开后利用基本不等式求最值;
的最小值时只要把“1”代入展开后利用基本不等式求最值;
命题②由已知求出向量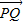 ,由
,由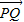 与
与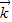 共线且|
共线且|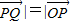 |列式得到动点P的轨迹;
|列式得到动点P的轨迹;
命题③利用M在平面MQR中,由共面向量基本定理得到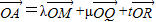 ,且λ+μ+t=1,由坐标相等得到
,且λ+μ+t=1,由坐标相等得到
λ,μ,t,则结论得证;
命题④由已知的向量得到向量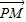 与
与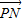 的坐标,利用条件
的坐标,利用条件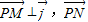 与
与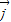 共线且|
共线且|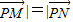 |,列式得到结论.
|,列式得到结论.
解答:解:对于①,由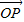 =
=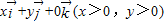 且|
且|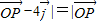
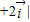 ,
,
所以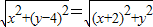 ,即
,即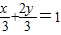 .
.
又x>0,y>0.所以 =
=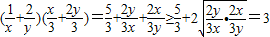 .
.
所以命题①不成立;
对于②,由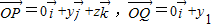
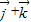 ,
,
所以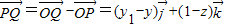 .
.
由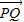 与
与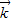 共线且|
共线且|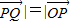 |,得
|,得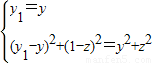 ,
,
整理得:y2=-2z+1.
所以动点P的轨迹是抛物线,命题②正确;
对于③,由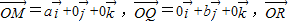 =
=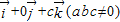 ,则平面MQR内的任意一点
,则平面MQR内的任意一点
A(x,y,z)满足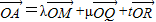 ,即(x,y,z)=λ(a,0,0)+μ(0,b,0)+t(0,0,c)
,即(x,y,z)=λ(a,0,0)+μ(0,b,0)+t(0,0,c)
所以x=λa,y=μb,z=tc.所以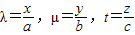 .
.
由λ+μ+t=1,得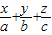 =1.所以③正确;
=1.所以③正确;
对于④,由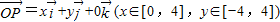 ,
,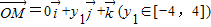 ,
,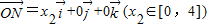 ,得
,得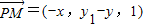 ,
,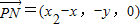 .
.
由向量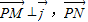 与
与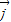 共线且|
共线且|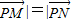 |,得
|,得
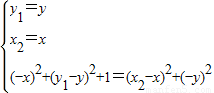 ,整理得:y2-x2=1(0≤x≤4,-4≤y≤4).
,整理得:y2-x2=1(0≤x≤4,-4≤y≤4).
所以动点P的轨迹是双曲线的一部分,所以④正确.
故正确的答案为②③④.
点评:本题考查了圆锥曲线的轨迹问题,考查了向量的共线即垂直的条件,考查了空间向量的坐标加法与减法运算,该题题目叙述冗长,考查了学生的读题能力,属有一定难度题目.
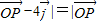
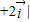 得到两个正数x,y的关系
得到两个正数x,y的关系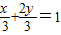 ,求
,求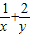 的最小值时只要把“1”代入展开后利用基本不等式求最值;
的最小值时只要把“1”代入展开后利用基本不等式求最值;命题②由已知求出向量
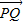 ,由
,由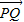 与
与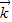 共线且|
共线且|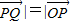 |列式得到动点P的轨迹;
|列式得到动点P的轨迹;命题③利用M在平面MQR中,由共面向量基本定理得到
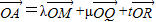 ,且λ+μ+t=1,由坐标相等得到
,且λ+μ+t=1,由坐标相等得到λ,μ,t,则结论得证;
命题④由已知的向量得到向量
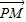 与
与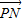 的坐标,利用条件
的坐标,利用条件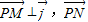 与
与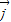 共线且|
共线且|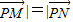 |,列式得到结论.
|,列式得到结论.解答:解:对于①,由
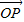 =
=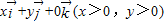 且|
且|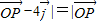
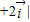 ,
,所以
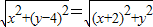 ,即
,即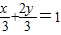 .
.又x>0,y>0.所以
 =
=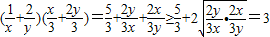 .
.所以命题①不成立;
对于②,由
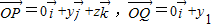
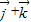 ,
,所以
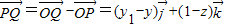 .
.由
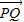 与
与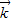 共线且|
共线且|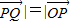 |,得
|,得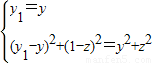 ,
,整理得:y2=-2z+1.
所以动点P的轨迹是抛物线,命题②正确;
对于③,由
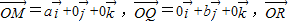 =
=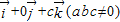 ,则平面MQR内的任意一点
,则平面MQR内的任意一点A(x,y,z)满足
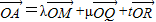 ,即(x,y,z)=λ(a,0,0)+μ(0,b,0)+t(0,0,c)
,即(x,y,z)=λ(a,0,0)+μ(0,b,0)+t(0,0,c)所以x=λa,y=μb,z=tc.所以
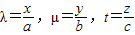 .
.由λ+μ+t=1,得
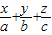 =1.所以③正确;
=1.所以③正确;对于④,由
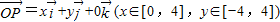 ,
,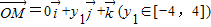 ,
,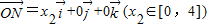 ,得
,得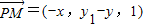 ,
,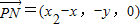 .
.由向量
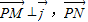 与
与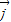 共线且|
共线且|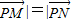 |,得
|,得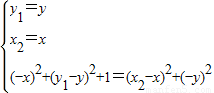 ,整理得:y2-x2=1(0≤x≤4,-4≤y≤4).
,整理得:y2-x2=1(0≤x≤4,-4≤y≤4).所以动点P的轨迹是双曲线的一部分,所以④正确.
故正确的答案为②③④.
点评:本题考查了圆锥曲线的轨迹问题,考查了向量的共线即垂直的条件,考查了空间向量的坐标加法与减法运算,该题题目叙述冗长,考查了学生的读题能力,属有一定难度题目.

练习册系列答案
相关题目