Question

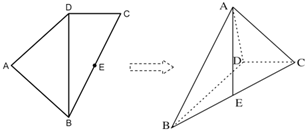如图，左边四边形ABCD中，E是BC的中点，DB=2，DC=1，BC=

5

，AB=AD=

2

，将左图沿直线BC折起，使得二面角A-BC-C为60°．如图
（1）求证：AE⊥平面BDC；
（2）求直线AC与平面ABD所成角的余弦值．

Answer 1

分析：（1）取BD中点F，连结EF，AF，由余弦定理及勾股定理，可得AE⊥EF，由线面垂直的性质可得BD⊥AE，由线面垂直的判定定理可得AE⊥平面BDC；
（2）以E为原点建立如图示的空间直角坐标系，求出直线AC的方向向量与平面ABD的法向量，代入向量夹角公式，可得直线AC与平面ABD所成角的余弦值．

解答：证明：（1）取BD中点F，连结EF，AF，
则AF=1，EF=

1

2

，∠AFE=60°，（2分），
由余弦定理知：
AE=

12+( 1 2 )2-2•1• 1 2 cos60°

=

3

2

，
∵AF²+EF²=AE²，
∴AE⊥EF，（4分），
又BD⊥平面AEF，AE?平面AEF，
∴BD⊥AE，
又∵EF∩BD=F，EF，BD?平面BDC
∴AE⊥平面BDC；      （6分）
解：（2）以E为原点建立如图示的空间直角坐标系，
则A(0，0，

3

2

)，C(-1，

1

2

，0)，B(1，-

1

2

，0)，D(-1，-

1

2

，0)，（8分），
设平面ABD的法向量为

n

=（x，y，z），
由

n • DB =0 n • DA =0

，得

2x=0 x+ 1 2 y+ 3 2 z=0

，
取z=

3

，则y=-3，
∴

n

=(0，-3，

3

)．
∵

AC

=(-1，

1

2

，-

3

2

)，
∴cos＜n，

AC

＞=

n• AC

|n|| AC |

=-

6

4

（11分）
故直线AC与平面ABD所成角的余弦值为

10

4

．（12分）

点评：本题考查的知识点是直线与平面所成的角，直线与平面垂直的判定，解答（1）的关键是熟练掌握线面垂直的判定定理，解答（2）的关键是建立空间坐标系，将线面夹角问题转化为向量夹角问题．