题目内容
已知函数
(1)试判断函数f(x)的单调性;
(2)设m>0,求f(x)在[m,2m]上的最大值;
(3)试证明:对?n∈N*,不等式 .
.
解:(1)函数f(x)的定义域是:(0,+∞)
由已知
令f′(x)=0得,1-lnx=0,∴x=e
∵当0<x<e时, ,
,
当x>e时,
∴函数f(x)在(0,e]上单调递增,在[e,+∞)上单调递减,
(2)由(1)知函数f(x)在(0,e]上单调递增,在[e,+∞)上单调递减
故①当0<2m≤e即 时,f(x)在[m,2m]上单调递增
时,f(x)在[m,2m]上单调递增
∴ ,
,
②当m≥e时,f(x)在[m,2m]上单调递减
∴ ,
,
③当m<e<2m,即 时
时
∴ .
.
(3)由(1)知,当x∈(0,+∞)时, ,
,
∴在(0,+∞)上恒有 ,
,
即 且当x=e时“=”成立,
且当x=e时“=”成立,
∴对?x∈(0,+∞)恒有 ,
,
∵ ,
,
∴
即对?n∈N*,不等式 恒成立.
恒成立.
分析:(1)利用商的求导法则求出所给函数的导函数是解决本题的关键,利用导函数的正负确定出函数的单调性;
(2)利用导数作为工具求出函数在闭区间上的最值问题,注意分类讨论思想的运用;
(3)利用导数作为工具完成该不等式的证明,注意应用函数的最值性质.
点评:本题考查导数在函数中的应用问题,考查函数的定义域思想,考查导数的计算,考查导数与函数单调性的关系,考查函数的最值与导数的关系,注意问题的等价转化性.
由已知

令f′(x)=0得,1-lnx=0,∴x=e
∵当0<x<e时,
 ,
,当x>e时,

∴函数f(x)在(0,e]上单调递增,在[e,+∞)上单调递减,
(2)由(1)知函数f(x)在(0,e]上单调递增,在[e,+∞)上单调递减
故①当0<2m≤e即
 时,f(x)在[m,2m]上单调递增
时,f(x)在[m,2m]上单调递增∴
 ,
,②当m≥e时,f(x)在[m,2m]上单调递减
∴
 ,
,③当m<e<2m,即
 时
时∴
 .
.(3)由(1)知,当x∈(0,+∞)时,
 ,
,∴在(0,+∞)上恒有
 ,
,即
 且当x=e时“=”成立,
且当x=e时“=”成立,∴对?x∈(0,+∞)恒有
 ,
,∵
 ,
,∴

即对?n∈N*,不等式
 恒成立.
恒成立.分析:(1)利用商的求导法则求出所给函数的导函数是解决本题的关键,利用导函数的正负确定出函数的单调性;
(2)利用导数作为工具求出函数在闭区间上的最值问题,注意分类讨论思想的运用;
(3)利用导数作为工具完成该不等式的证明,注意应用函数的最值性质.
点评:本题考查导数在函数中的应用问题,考查函数的定义域思想,考查导数的计算,考查导数与函数单调性的关系,考查函数的最值与导数的关系,注意问题的等价转化性.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
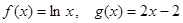 .
.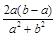 (闭区间[m,n]的长度定义为n –m).
(闭区间[m,n]的长度定义为n –m).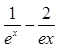 是否存在实数根?说明理由。
是否存在实数根?说明理由。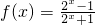
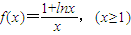
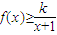 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;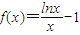
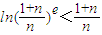 .
.