题目内容
11.若i是虚数单位,Z的共轭复数$\overline{Z}$,复数z=$\frac{-1+3i}{1+2i}$,则$\overline Z$在复平面对应的点为( )| A. | (5,5) | B. | (5,-5) | C. | (1,1) | D. | (1,-1) |
分析 利用复数的运算法则、共轭复数的定义即可得出.
解答 解:复数z=$\frac{-1+3i}{1+2i}$=$\frac{(-1+3i)(1-2i)}{(1+2i)(1-2i)}$=$\frac{5+5i}{5}$=1+i,
则$\overline Z$=1-i在复平面对应的点为(1,-1).
故选:D.
点评 本题考查了复数的运算法则、共轭复数的定义,考查了计算能力,属于基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
19.已知随机变量ξ的分布列为ξ=-1,0,1,对应P=$\frac{1}{2}$,$\frac{1}{6}$,$\frac{1}{3}$,且设η=2ξ+1,则η的期望为( )
| A. | -$\frac{1}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{29}{36}$ | D. | 1 |
6.随机变量ξ服从正态分布N(2,σ2),P(ξ≤4)=0.84,则P(ξ<0)=( )
| A. | 0.16 | B. | 0.32 | C. | 0.68 | D. | 0.84 |
16.设α,β为两个不同的平面,n,m为两条不同的直线,且n?α,m?β,有如下两个命题:
p:若α∥β,则n∥m;
q:若m⊥n,则α⊥β,那么( )
p:若α∥β,则n∥m;
q:若m⊥n,则α⊥β,那么( )
| A. | p∧q是假命题 | B. | p∨q是真命题 | C. | ¬p是假命题 | D. | p∧(¬q)是真命题 |
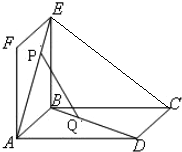 如图:已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,求证:PQ∥面CBE.
如图:已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,求证:PQ∥面CBE.