Question

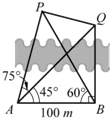（2013•辽宁二模）风景秀美的凤凰湖畔有四棵高大的银杏树，记做A、B、P、Q，欲测量P、Q两棵树和A、P两棵树之间的距离，但湖岸部分地方围有铁丝网不能靠近，现在可以方便的测得A、B两点间的距离为AB=100米，如图，同时也能测量出∠PAB=75°，∠QAB=45°，∠PBA=60°，∠QBA=90°，则P、Q两棵树和A、P两棵树之间的距离各为多少？

Answer 1

分析：在三角形PAB中，由内角和定理求出∠APB的度数，由sin∠APB，sin∠ABC，以及AB的长，利用正弦定理求出AP的长即可；在三角形QAB中，由∠ABQ为直角，∠CAB为45度，得到三角形QAB为等腰直角三角形，根据AB求出AQ的长，∠PAQ的度数，利用余弦定理即可求出PQ的长．

解答：解：在△PAB中，∠APB=180°-（75°+60°）=45°，
由正弦定理得：

AP

sin60°

=

100

sin45°

，得到AP=50

6

（米）；
在△QAB中，∠ABQ=90°，∠CAB=45°，AB=100米，
∴AQ=100

2

米，∠PAQ=75°-45°=30°，
由余弦定理得：PQ²=（50

6

）²+（100

2

）²-2×50

6

×100

2

cos30°=5000，
解得：PQ=50

2

，
答：P、Q两颗树之间的距离为50

2

米，A、P两颗树之间的距离为50

6

米．

点评：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．