题目内容
对于函数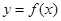 ,若存在区间
,若存在区间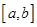 ,当
,当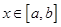 时的值域为
时的值域为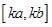
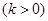 ,则称
,则称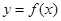 为
为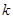 倍值函数.若
倍值函数.若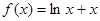 是
是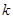 倍值函数,则实数
倍值函数,则实数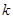 的取值范围是 。
的取值范围是 。
【答案】

【解析】
试题分析: 的定义域为
的定义域为 ,且在在定义域内为单调增函数,
,且在在定义域内为单调增函数,
因此有: 即:
即:
即 为方程
为方程 的两个不同实数根,所以
的两个不同实数根,所以 ,
,
令 ,由
,由 ,得极大值点为
,得极大值点为
 的极大值为:
的极大值为: ,又因为
,又因为 时,
时, ,
, 时,
时, ,因此当
,因此当 时,
时, 有两个解。
有两个解。
故所求的 的取值范围为
的取值范围为 .
.
考点:本小题主要考查新定义下函数的值域问题和函数的极值最值问题,考查学生的转化问题的能力和分类讨论思想的应用以及运算求解能力.
点评:对于新定义问题,要根据题意将问题适当的转化为熟悉的数学问题求解.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
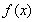
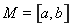
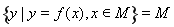
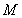
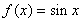
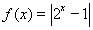
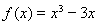
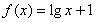
 ,若存在区间
,若存在区间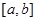 ,当
,当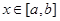 时,函数
时,函数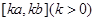 ,则称
,则称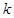 倍值函数. 若
倍值函数. 若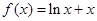 是
是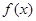 ,若存在区间
,若存在区间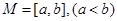 ,使得
,使得 ,则称区间
,则称区间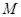 为函数
为函数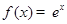 ; ②
; ②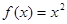 ③
③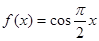 ④
④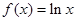 .其中存在“稳定区间”的函数的个数为(
)
.其中存在“稳定区间”的函数的个数为(
)
 ,若存在区间
,若存在区间 ,使得
,使得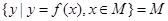 ,则称区间
,则称区间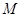 为函数
为函数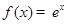 ; ②
; ②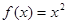 ③
③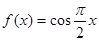 ④
④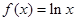 .其中存在“稳定区间”的函数的个数为
.其中存在“稳定区间”的函数的个数为