题目内容
设 在区间
在区间 上有定义, 若
上有定义, 若
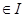 , 都有
, 都有 , 则称
, 则称 是区间
是区间 的向上凸函数;若
的向上凸函数;若
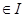 , 都有
, 都有 , 则称
, 则称 是区间
是区间 的向下凸函数. 有下列四个判断:
的向下凸函数. 有下列四个判断:
①若 是区间
是区间 的向上凸函数,则
的向上凸函数,则 是区间
是区间 的向下凸函数;
的向下凸函数;
②若 和
和 都是区间
都是区间 的向上凸函数, 则
的向上凸函数, 则 是区间
是区间 的向上凸函数;
的向上凸函数;
③若 在区间
在区间 的向下凸函数且
的向下凸函数且 ,则
,则 是区间
是区间 的向上凸函数;
的向上凸函数;
④若 是区间
是区间 的向上凸函数,
的向上凸函数, , 则有
, 则有

其中正确的结论个数是( )
A.1 B.2 C.3 D.4
【答案】
①②
【解析】
试题分析:利用定义易知正确,③反例

因为 
 所以④正确.故填写①②。
所以④正确.故填写①②。
考点:函数的性质
点评:主要是对于新定义的理解和运用,属于中档题。

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目