题目内容
已知数列{an}的前n项和为Sn,点(n,Sn)在函数f(x)=2x-1的图象上,数列{bn}满足bn=log2an-12(n∈N*).(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Tn,当Tn最小时,求n的值;
(3)求不等式Tn<bn的解集.
【答案】分析:(1)把点(n,Sn)代入函数f(x)=2x-1得到数列的前n项和,然后由an=Sn-Sn-1求解n≥2使得数列通项,最后验证n=1时是否成立;
(2)把数列{an}的通项公式代入bn=log2an-12,得到数列{bn}为等差数列,求出首项和公差,则其前n项和得到表示,利用二次函数求使其前n项和取最小值时的n值;
(3)直接把Tn和bn的代数式代入Tn<bn化为一元二次不等式求解.
解答:(1)依题意:Sn=2n-1(n∈N*),
∴当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1.
当n=1,S1=a1=1,∴an=2n-1(n∈N*);
(2)因为bn=log2an-12=n-13,
所以b1=-12,d=bn-bn-1=(n-13)-(n-1-13)=1.
所以数列{bn}是以-12为首项,以1为公差的等差数列.
∴Tn=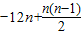 =
=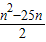 =
= (n-
(n-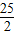 )2-
)2-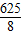 .
.
故当n=12或13时,数列{bn}的前n项和最小;
(3)由Tn-bn=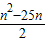 -(n-13)=
-(n-13)=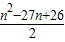
=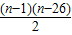 <0,
<0,
∴1<n<26,且n∈N*,
所以不等式的解集为{n|1<n<26,n∈N*}.
点评:本题考查了等差数列的通项公式的求法,考查了分类讨论的数学思想方法,考查了等差数列的前n项和公式及一元二次不等式的解法,是中档题.
(2)把数列{an}的通项公式代入bn=log2an-12,得到数列{bn}为等差数列,求出首项和公差,则其前n项和得到表示,利用二次函数求使其前n项和取最小值时的n值;
(3)直接把Tn和bn的代数式代入Tn<bn化为一元二次不等式求解.
解答:(1)依题意:Sn=2n-1(n∈N*),
∴当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1.
当n=1,S1=a1=1,∴an=2n-1(n∈N*);
(2)因为bn=log2an-12=n-13,
所以b1=-12,d=bn-bn-1=(n-13)-(n-1-13)=1.
所以数列{bn}是以-12为首项,以1为公差的等差数列.
∴Tn=
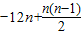 =
=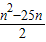 =
= (n-
(n-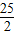 )2-
)2-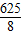 .
.故当n=12或13时,数列{bn}的前n项和最小;
(3)由Tn-bn=
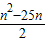 -(n-13)=
-(n-13)=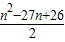
=
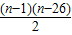 <0,
<0,∴1<n<26,且n∈N*,
所以不等式的解集为{n|1<n<26,n∈N*}.
点评:本题考查了等差数列的通项公式的求法,考查了分类讨论的数学思想方法,考查了等差数列的前n项和公式及一元二次不等式的解法,是中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |