题目内容
某商场搞促销,当顾客购买商品的金额达到一定数量之后可以抽奖,根据顾客购买商品的金额,从箱中(装有4只红球,3只白球,且除颜色外,球的外部特征完全相同)每抽到一只红球奖励20元的商品,每抽到一只白球奖励10元的商品(当顾客通过抽奖的方法确定了获奖商品后,即将小球全部放回箱中).
(1)当顾客购买金额超过500元而少于1000元(含1000元)时,可从箱中一次随机抽取3个小球,求其中至少有一个红球的概率;
(2)当顾客购买金额超过1000元时,可一次随机抽取4个小球,设他所获奖商品的金额为ξ元,求ξ的概率分布列和数学期望.
(1)当顾客购买金额超过500元而少于1000元(含1000元)时,可从箱中一次随机抽取3个小球,求其中至少有一个红球的概率;
(2)当顾客购买金额超过1000元时,可一次随机抽取4个小球,设他所获奖商品的金额为ξ元,求ξ的概率分布列和数学期望.
解:(1)基本事件总数n= =35,
=35,
设事件A={任取3球,至少有一个红球},则事件 ={任取3球,全是白球},
={任取3球,全是白球},
∴P( )=
)= ,
,
∵A与 为对立事件,
为对立事件,
于是P(A)=1-P( )=
)= ,
,
即该顾客任取3球,至少有一个红球的概率为 。
。
(2)依题意,ξ的可能取值为50,60,70,80,
ξ=50表示所取4球为3白1红(3×10+1×20=50),
∴P(ξ=50)= ,
,
ξ=60表示所取4球为2白2红(2×10+2×20=60),
∴P(ξ=60)= ,
,
ξ=70表示所取4球为3红1白(3×20+1×10=70),
∴P(ξ=70)= ,
,
ξ=80表示所取4球全为红球(4×20=80),
∴P(ξ=80)= ,
,
于是ξ的分布列为:

∴Eξ= (元),
(元),
即该顾客获奖的期望是 ≈63(元).
≈63(元).
 =35,
=35,设事件A={任取3球,至少有一个红球},则事件
 ={任取3球,全是白球},
={任取3球,全是白球},∴P(
 )=
)= ,
,∵A与
 为对立事件,
为对立事件,于是P(A)=1-P(
 )=
)= ,
,即该顾客任取3球,至少有一个红球的概率为
 。
。(2)依题意,ξ的可能取值为50,60,70,80,
ξ=50表示所取4球为3白1红(3×10+1×20=50),
∴P(ξ=50)=
 ,
,ξ=60表示所取4球为2白2红(2×10+2×20=60),
∴P(ξ=60)=
 ,
,ξ=70表示所取4球为3红1白(3×20+1×10=70),
∴P(ξ=70)=
 ,
,ξ=80表示所取4球全为红球(4×20=80),
∴P(ξ=80)=
 ,
,于是ξ的分布列为:

∴Eξ=
 (元),
(元),即该顾客获奖的期望是
 ≈63(元).
≈63(元). 
练习册系列答案
相关题目
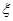 元,求
元,求 元,求
元,求 元,求
元,求 元,求
元,求