题目内容
函数f(x)=x2+bln(x+1)﹣2x,b∈R
(I)当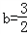 时,求函数f(x)的极值;
时,求函数f(x)的极值;
(II)设g(x)=f(x)+2x,若b≥2,求证:对任意x1,x2∈(﹣1,+∞),且x1≥x2,都有g(x1)﹣g(x2)≥2(x1﹣x2).
(I)当
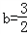 时,求函数f(x)的极值;
时,求函数f(x)的极值;(II)设g(x)=f(x)+2x,若b≥2,求证:对任意x1,x2∈(﹣1,+∞),且x1≥x2,都有g(x1)﹣g(x2)≥2(x1﹣x2).
解:(1)当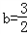 时,函数解析式为
时,函数解析式为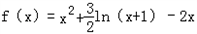 ,定义域为(﹣1,+∞)
,定义域为(﹣1,+∞)
∴对函数求导数,得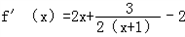 ,
,
令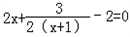 ,解得
,解得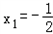 或
或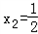
当x变化时,f'(x),f(x)的变化情况如下表:
(2)因为f(x)=x2+bln(x+1)﹣2x,
所以 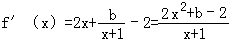 ,其中x∈(﹣1,+∞)
,其中x∈(﹣1,+∞)
因为b≥2,所以f'(x)≥0(当且仅当b=2,x=0时等号成立),
所以f(x)在区间(﹣1,+∞)上是增函数,
从而对任意x1,x2∈(﹣1,+∞),
当x1≥x2时,f(x1)≥f(x2),
又∵g(x)=f(x)+2x,
∴g(x1)=f(x1)+2x1,g(x2)=f(x2)+2x2
即g(x1)+2x1≥g(x2)+2x2,整理得g(x1)﹣g(x2)≥2(x1﹣x2)
所以对任意x1,x2∈(﹣1,+∞),且x1≥x2,
都有g(x1)﹣g(x2)≥2(x1﹣x2).

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目