题目内容
已知函数f(x)=lg(x+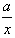 -2),其中a是大于0的常数,
-2),其中a是大于0的常数,
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)当a∈(1,4)时,求函数f(x)在[2,+∞)上的最小值;
(Ⅲ)若对任意x∈[2,+∞)恒有f(x)>0,试确定a的取值范围。
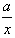 -2),其中a是大于0的常数,
-2),其中a是大于0的常数,(Ⅰ)求函数f(x)的定义域;
(Ⅱ)当a∈(1,4)时,求函数f(x)在[2,+∞)上的最小值;
(Ⅲ)若对任意x∈[2,+∞)恒有f(x)>0,试确定a的取值范围。
解:(Ⅰ)由题意, ,即x(x2-2x+a)>0,
,即x(x2-2x+a)>0,
ⅰ)当Δ=4-4a<0,即a>1时,x2-2x+a>0恒成立,故定义域为(0,+∞);
ⅱ)当Δ=4-4a=0,即a=1时,定义域为(0,1)∪(1,+∞);
ⅲ)当Δ=4-4a>0,即a<1时, ,
,
即定义域为 ;
;
(Ⅱ)∵1<a<4, 在
在 上递减,
上递减, 上递增,
上递增,
又 ,
,
∴ 在[2,+∞)上递增,
在[2,+∞)上递增,
∴ 。
。
(Ⅲ)f(x)>0 ,即a>(3-x)x在[2,+∞)恒成立,
,即a>(3-x)x在[2,+∞)恒成立,
t=-x2+3x(x≥2)的最大值为2,
∴a>2。
 ,即x(x2-2x+a)>0,
,即x(x2-2x+a)>0, ⅰ)当Δ=4-4a<0,即a>1时,x2-2x+a>0恒成立,故定义域为(0,+∞);
ⅱ)当Δ=4-4a=0,即a=1时,定义域为(0,1)∪(1,+∞);
ⅲ)当Δ=4-4a>0,即a<1时,
 ,
,即定义域为
 ;
;(Ⅱ)∵1<a<4,
 在
在 上递减,
上递减, 上递增,
上递增,又
 ,
,∴
 在[2,+∞)上递增,
在[2,+∞)上递增, ∴
 。
。(Ⅲ)f(x)>0
 ,即a>(3-x)x在[2,+∞)恒成立,
,即a>(3-x)x在[2,+∞)恒成立,t=-x2+3x(x≥2)的最大值为2,
∴a>2。

练习册系列答案
相关题目