题目内容
若a>1,设函数f(x)=ax+x-4的零点为m,g(x)=logax+x-4的零点为n,则
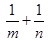
的取值范围( )
A.(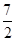 ,+∞) B.(1,+∞) C.(4,+∞) D.(9 ,+∞)
,+∞) B.(1,+∞) C.(4,+∞) D.(9 ,+∞)
【答案】
B
【解析】解:函数f(x)=ax+x-4的零点是函数y=ax与函数y=4-x图象交点A的横坐标,
函数g(x)=logax+x-4的零点是函数y=logax与函数y=4-x图象交点B的横坐标,
由于指数函数与对数函数互为反函数,
其图象关于直线y=x对称,
直线y=4-x与直线y=x垂直,
故直线y=4-x与直线y=x的交点(2,2)即是A,B的中点,
∴m+n=4,
∴ =
= ,(m+n)(
,(m+n)(
 )=
)=
 (2+
(2+
 )≥1,
)≥1,
但这里m≠n,
故所求的取值范围是(1,+∞).
故选B.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
若a>1,设函数f(x)=ax+x-4的零点为m,g(x)=logax+x-4的零点为n,则
+
的取值范围( )
| 1 |
| m |
| 1 |
| n |
A、(
| ||
| B、(1,+∞) | ||
| C、(4,+∞) | ||
D、(
|
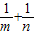 的取值范围( )
的取值范围( )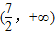
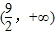
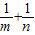 的取值范围( )
的取值范围( )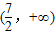
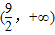
 的取值范围( )
的取值范围( )
