题目内容
已知函数 (a>0,a≠1,m≠1)是奇函数.
(a>0,a≠1,m≠1)是奇函数.
(1)求实数m的值;
(2)当x∈(n,a-2)时,函数f(x)的值域是(1,+∞),求实数a与n的值;
(3)令函数g(x)=-ax2+8(x-1)af(x)-5,试问是否存在实数a,使得对任意的实数x∈(1,2],-5≤g(x)≤5恒成立?若存在,求出实数a的取值范围;若不存在,说明理由.
解:(1)由函数 (a>0,a≠1,m≠1)是奇函数
(a>0,a≠1,m≠1)是奇函数
得f(-x)+f(x)=0对定义域中的任意实数x均成立.
∴ .
.
即
即m2x2-1=x2-1对定义域中的任意实数x均成立.
∴m2=1即m=1(舍去)或m=-1.
∴m=-1.
(2)因为函数f(x)的定义域为(1,+∞)∪(-∞,-1),
∴①当n<a-2≤-1时,0<a<1,
∴f(x)在区间(n,a-2)上为增函数,
要使值域为(1,+∞),则 (无解);
(无解);
②当1≤n<a-2时,a>3,
∴f(x)在区间(n,a-2)上为减函数,
要使f(x)的值域为(1,+∞),则 ,
,
∴ ,n=1.
,n=1.
(3)g(x)=-ax2+8(x-1)af(x)-5=-ax2+8x+3,
假设存在实数a,使得对任意的实数x∈(1,2],-5≤g(x)≤5恒成立,
则有 对任意的实数x∈(1,2]恒成立,
对任意的实数x∈(1,2]恒成立,
即 对任意的实数x∈(1,2]恒成立,
对任意的实数x∈(1,2]恒成立,
令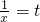 ,则有
,则有 对任意的实数
对任意的实数 恒成立,
恒成立,
因为函数8(t2+t)在 上递增,所以函数8(t2+t)的最小值为6,
上递增,所以函数8(t2+t)的最小值为6,
所以 a≤6;
因为函数8t-2t2在 上递增,所以函数8t-2t2<6,
上递增,所以函数8t-2t2<6,
所以a≥6.
综上,a=6
所以,存在a=6使得对任意的实数x∈(1,2],-5≤g(x)≤5恒成立.
分析:(1)由函数 (a>0,a≠1,m≠1)是奇函数得f(-x)+f(x)=0对定义域中的任意实数x均成立,代入可求m
(a>0,a≠1,m≠1)是奇函数得f(-x)+f(x)=0对定义域中的任意实数x均成立,代入可求m
(2)因为函数f(x)的定义域为(1,+∞)∪(-∞,-1),需要考虑(n,a-2)与定义域的关系,故分类讨论①当n<a-2≤-1时,0<a<1,②当1≤n<a-2时,a>3,分别求解函数的值域即可
(3)由题意可得g(x)=-ax2+8x+3,假设存在实数a,使得对任意的实数x∈(1,2],-5≤g(x)≤5恒成立,则有 对任意的实数x∈(1,2]恒成立,即
对任意的实数x∈(1,2]恒成立,即  对任意的实数x∈(1,2]恒成立,结合二次函数的性质可求
对任意的实数x∈(1,2]恒成立,结合二次函数的性质可求
点评:本题主要考查了奇函数的定义的应用,函数的值域的求解,体现了分类讨论思想的应用,解决本题(3)的关键在于“转化”,先将转化为恒成立问题,再以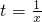 将问题转化为二次函数问题,最终得以解决
将问题转化为二次函数问题,最终得以解决
 (a>0,a≠1,m≠1)是奇函数
(a>0,a≠1,m≠1)是奇函数得f(-x)+f(x)=0对定义域中的任意实数x均成立.
∴
 .
.即

即m2x2-1=x2-1对定义域中的任意实数x均成立.
∴m2=1即m=1(舍去)或m=-1.
∴m=-1.
(2)因为函数f(x)的定义域为(1,+∞)∪(-∞,-1),
∴①当n<a-2≤-1时,0<a<1,
∴f(x)在区间(n,a-2)上为增函数,
要使值域为(1,+∞),则
 (无解);
(无解);②当1≤n<a-2时,a>3,
∴f(x)在区间(n,a-2)上为减函数,
要使f(x)的值域为(1,+∞),则
 ,
,∴
 ,n=1.
,n=1.(3)g(x)=-ax2+8(x-1)af(x)-5=-ax2+8x+3,
假设存在实数a,使得对任意的实数x∈(1,2],-5≤g(x)≤5恒成立,
则有
 对任意的实数x∈(1,2]恒成立,
对任意的实数x∈(1,2]恒成立,即
 对任意的实数x∈(1,2]恒成立,
对任意的实数x∈(1,2]恒成立,令
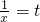 ,则有
,则有 对任意的实数
对任意的实数 恒成立,
恒成立,因为函数8(t2+t)在
 上递增,所以函数8(t2+t)的最小值为6,
上递增,所以函数8(t2+t)的最小值为6,所以 a≤6;
因为函数8t-2t2在
 上递增,所以函数8t-2t2<6,
上递增,所以函数8t-2t2<6,所以a≥6.
综上,a=6
所以,存在a=6使得对任意的实数x∈(1,2],-5≤g(x)≤5恒成立.
分析:(1)由函数
 (a>0,a≠1,m≠1)是奇函数得f(-x)+f(x)=0对定义域中的任意实数x均成立,代入可求m
(a>0,a≠1,m≠1)是奇函数得f(-x)+f(x)=0对定义域中的任意实数x均成立,代入可求m(2)因为函数f(x)的定义域为(1,+∞)∪(-∞,-1),需要考虑(n,a-2)与定义域的关系,故分类讨论①当n<a-2≤-1时,0<a<1,②当1≤n<a-2时,a>3,分别求解函数的值域即可
(3)由题意可得g(x)=-ax2+8x+3,假设存在实数a,使得对任意的实数x∈(1,2],-5≤g(x)≤5恒成立,则有
 对任意的实数x∈(1,2]恒成立,即
对任意的实数x∈(1,2]恒成立,即  对任意的实数x∈(1,2]恒成立,结合二次函数的性质可求
对任意的实数x∈(1,2]恒成立,结合二次函数的性质可求点评:本题主要考查了奇函数的定义的应用,函数的值域的求解,体现了分类讨论思想的应用,解决本题(3)的关键在于“转化”,先将转化为恒成立问题,再以
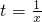 将问题转化为二次函数问题,最终得以解决
将问题转化为二次函数问题,最终得以解决 
练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
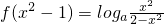 (a>0且a≠1).
(a>0且a≠1). (a>0,a≠1)的图象恒过定点A,若点A也在函数f(x)=3x+b的图象上,则b= .
(a>0,a≠1)的图象恒过定点A,若点A也在函数f(x)=3x+b的图象上,则b= . 其中a>0,且a≠1,
其中a>0,且a≠1, 的定义域;
的定义域; ;
; 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. =loga
=loga (a>0且a≠1)是奇函数
(a>0且a≠1)是奇函数 ,(
,(