题目内容
若函数f(x)=3sin(2x+φ)对任意x都有 ,φ的最小正值为
,φ的最小正值为
- A.
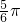
- B.

- C.

- D.

A
分析:由题意可得函数的对称轴为 x= ,根据2×
,根据2× +φ=kπ+
+φ=kπ+ ,k∈z 求得φ的最小正值.
,k∈z 求得φ的最小正值.
解答:∵函数f(x)=3sin(2x+φ)对任意x都有 ,故函数的对称轴为 x=
,故函数的对称轴为 x= ,
,
故有 2× +φ=kπ+
+φ=kπ+ ,k∈z.
,k∈z.
故φ的最小正值为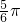 ,
,
故选A.
点评:本题主要考查正弦函数的图象的对称性,判断函数的对称轴为 x= ,是解题的关键,属于中档题.
,是解题的关键,属于中档题.
分析:由题意可得函数的对称轴为 x=
 ,根据2×
,根据2× +φ=kπ+
+φ=kπ+ ,k∈z 求得φ的最小正值.
,k∈z 求得φ的最小正值.解答:∵函数f(x)=3sin(2x+φ)对任意x都有
 ,故函数的对称轴为 x=
,故函数的对称轴为 x= ,
,故有 2×
 +φ=kπ+
+φ=kπ+ ,k∈z.
,k∈z.故φ的最小正值为
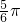 ,
,故选A.
点评:本题主要考查正弦函数的图象的对称性,判断函数的对称轴为 x=
 ,是解题的关键,属于中档题.
,是解题的关键,属于中档题. 
练习册系列答案
相关题目
 如图,M是单位圆与x轴正半轴的交点,点P在单位圆上,
如图,M是单位圆与x轴正半轴的交点,点P在单位圆上, 如图,M是单位圆与x轴正半轴的交点,点P在单位圆上,
如图,M是单位圆与x轴正半轴的交点,点P在单位圆上,