题目内容
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为| 1 | 6 |
(Ⅰ)求甲中奖且乙、丙都没有中奖的概率;
(Ⅱ)求中奖人数ξ的分布列及数学期望Eξ.
分析:(1)甲、乙、丙三位同学每人是否中奖相互独立,可利用独立事件的概率求解,甲中奖概率为
,乙、丙没有中奖的概率为
,相乘即可.
(2)中奖人数ξ的所有取值为0,1,2,3,是二项分布.ξ~B(3,
)
| 1 |
| 6 |
| 5 |
| 6 |
(2)中奖人数ξ的所有取值为0,1,2,3,是二项分布.ξ~B(3,
| 1 |
| 6 |
解答:解:(1)设甲、乙、丙中奖的事件分别为A、B、C,那么
P(A)=P(B)=P(C)=
,
P(A•
•
)=P(A)P(
)P(
)=
•(
)2=
,
答:甲中奖且乙、丙都没有中奖的概率为
.
(2)ξ的可能值为0,1,2,3,
P(ξ=k)=
(
)k(
)3-k(k=0,1,2,3)
所以中奖人数ξ的分布列为
Eξ=0×
+1×
+2×
+3×
=
.
P(A)=P(B)=P(C)=
| 1 |
| 6 |
P(A•
. |
| B |
. |
| C |
. |
| B |
. |
| C |
| 1 |
| 6 |
| 5 |
| 6 |
| 25 |
| 216 |
答:甲中奖且乙、丙都没有中奖的概率为
| 25 |
| 216 |
(2)ξ的可能值为0,1,2,3,
P(ξ=k)=
| C | k 3 |
| 1 |
| 6 |
| 5 |
| 6 |
所以中奖人数ξ的分布列为

Eξ=0×
| 125 |
| 216 |
| 25 |
| 72 |
| 5 |
| 72 |
| 1 |
| 216 |
| 1 |
| 2 |
点评:本题考查相互独立事件、互斥事件的概率、离散型随机变量的分布列、二项分布及期望等知识.同时考查利用所学知识分析问题解决问题的能力.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。 ,甲、乙、丙三位同学每人购买了一瓶该饮料。
,甲、乙、丙三位同学每人购买了一瓶该饮料。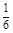 .甲、乙、丙三位同学每人购买了一瓶该饮料.
.甲、乙、丙三位同学每人购买了一瓶该饮料.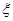 的分布列及数学期望
的分布列及数学期望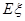 .
.