题目内容
（本题满分16分）已知
.
（1）已知
，分别求
的值；
（2）画出函数
的图像，并指出函数的单调区间（不要求证明）；
（3）解不等式
【答案】
（1）
.
（2）
分别在
上是增函数；
（3）
.
【解析】
试题分析：(1)根据分段函数x的不同的取值范围，对应关系不同，来分别求出
的值.
（2）分别画出
和
上的图像，从图像上找出其单调区间.
（3）由于f(x)是分段函数,所以
,然后解这两个不等式组求并集即可.
（1）
，
.
（2）图像……
，
分别在上是增函数……
（3）
……
或
……
.
……
.
考点：分段函数的图像，单调区间.
点评：分段函数在研究其单调性时要注意分段研究，解与它有关的不等式时，要注意分段求解，最后再求并集.
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
，且对任意
，有
.
；
在区间（0，1）上为单调函数，求实
数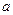
的取值范围.
的零点个数？(提示
)
为实常数）．
时，求函数
在
上的最小值；
在区间
上有解，求实数
的取值范围；
）
：
的离心率为
，
分别为椭圆
为椭圆上任意一点，以
为半径作圆
有公共点时，求△
面积的最大值．
是定义在
上的偶函数，且当
时，
。
及
的值；
上的解析式；
的方程
有四个不同的实数解，求实数
的取值范围。