题目内容
已知函数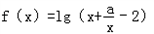 ,其中a是大于0的常数。
,其中a是大于0的常数。
(1)求函数f(x)的定义域;
(2)当a∈(1,4)时,求函数f(x)在[2,+∞)上的最小值;
(3)若对任意x∈[2,+∞)恒有f(x)>0,试确定a的取值范围。
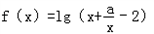 ,其中a是大于0的常数。
,其中a是大于0的常数。(1)求函数f(x)的定义域;
(2)当a∈(1,4)时,求函数f(x)在[2,+∞)上的最小值;
(3)若对任意x∈[2,+∞)恒有f(x)>0,试确定a的取值范围。
解:(1)由 得
得
解得a>1时,∞定义域为(0,+)
a=1时,定义域为{x|x>0且x≠1},
0<a<1时,定义域为 或
或 };
};
(2)设 ,
,
当a∈(1,4),x∈[2,+∞)时, 恒成立,
恒成立,
∴ 在[2,+∞)上是增函数,
在[2,+∞)上是增函数,
∵ 在[2,+∞)上是增函数,
在[2,+∞)上是增函数,
∴ 在[2,+∞)上的最小值为
在[2,+∞)上的最小值为 ;
;
(3)对任意x∈[2,+∞)恒有f(x)>0,
即 对x∈[2,+∞)恒成立
对x∈[2,+∞)恒成立
∴a>3x-x2,而 在x∈[2,+∞)上是减函数,
在x∈[2,+∞)上是减函数,
∴h(x)max=h(2)=2,
∴a>2。

练习册系列答案
相关题目
 ,其中a>0.
,其中a>0. 的单调区间;
的单调区间; 是曲线
是曲线 的切线,求实数a的值;
的切线,求实数a的值; ,求
,求 在区间
在区间 上的最大值(其中e为自然对的底数)。
上的最大值(其中e为自然对的底数)。 ,其中a>0.
,其中a>0. ,其中a>0.
,其中a>0. ,其中a>0.
,其中a>0.