题目内容
(12分)已知命题p： ∀x∈[1,2]，x3－a≥0. 命题q：∃x0∈R，使得x＋(a－1)x0＋1<0.若
p为假，p且q为假，求实数a的取值范围．
【答案】
解 ∵∀x∈[1,2]，x3－a≥0恒成立，
即a≤x3恒成立，∴a≤1.
即p：a≤1，
又∃x0∈R，使得x＋(a－1)x0＋1<0.
∴Δ＝(a－1)2－4>0，∴a>3或a<－1，
即q：a>3或a<－1，
又
p为假，p且q为假，∴p真q假
当p真q假时，{a|a≤1}∩{a|－1≤a≤3}＝{a|－1≤a≤1}．
a的取值范围为{a|－1≤a≤1}
【解析】略
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
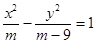表示焦点在y轴上的椭圆；命题q：双曲线
的离心率
，若p、q有且只有一个为真，求m的取值范围。
是R上的减函数，命题Q：在
时，不等式
恒成立，若命题“
”是真命题，求实数
的取值范围.
在
内有且仅有一个零点．命题q：
在区间
内恒成立．若命题“p且q”是假命题，求实数
的取值范围．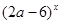
在R上单调递减; 命题q：关于x的方程
的两个实根均大于0，若
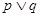为真，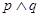
为假，求实数a的取值范围。