题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)设曲线![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,曲线在点
,曲线在点![]() 处的切线方程为
处的切线方程为![]() ,求证:对于任意的实数
,求证:对于任意的实数![]() ,都有
,都有![]() ;
;
(3)若方程![]() 为实数)有两个实数根
为实数)有两个实数根![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(1)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】
(1)求出原函数的导函数,求![]() 和
和![]() 的解,即可求出函数
的解,即可求出函数![]() 的单调性;
的单调性;
(2)设出点![]() 的坐标,利用导数求出切线方程
的坐标,利用导数求出切线方程![]() ,构造函数
,构造函数![]() ,利用导数得到对于任意实数
,利用导数得到对于任意实数![]() ,有
,有![]() ,即对任意实数
,即对任意实数![]() ,都有
,都有![]() ;
;
(3)由(2)知,![]() ,求出方程
,求出方程![]() 的根
的根![]() ,由
,由![]() 在
在![]() 上单调递减,得到
上单调递减,得到![]() .同理得到
.同理得到![]() ,则可证得结果..
,则可证得结果..
(1)解:由![]() ,可得
,可得![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减.
单调递减.
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)证明:设点![]() 的坐标为
的坐标为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() ,
,
令函数![]() ,即
,即![]() ,
,
则![]() ,
,![]() 在R上单调递减.
在R上单调递减.
![]() ,
,![]() 当
当![]() 时,
时,![]() ;当
;当![]() ,
,![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递减,
上单调递减,
![]() 对于任意实数
对于任意实数![]() ,
,![]() ,即对任意实数
,即对任意实数![]() ,都有
,都有![]() ;
;
(3)证明:由(2)知,![]() ,设方程
,设方程![]() 的根为
的根为![]() ,可得
,可得![]() .
.
![]() 在
在![]() 上单调递减,又由(2)知
上单调递减,又由(2)知![]() ,
,
因此![]() .
.
类似地,设曲线![]() 在原点处的切线方程为
在原点处的切线方程为![]() ,可得
,可得![]() ,
,
对于任意的![]() ,有
,有![]() ,即
,即![]() .
.
设方程![]() 的根为
的根为![]() ,可得
,可得![]() ,
,
![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,
因此![]() ,
,
由此可得![]() .
.

【题目】2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对于线上教育进行调查,其中男生与女生的人数之比为![]() ,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | |||
女生 | |||
合计 | 120 |
(2)从被调查中对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取2名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
参考公式:附: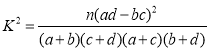
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.842 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】过椭圆![]() 的左顶点
的左顶点![]() 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设动直线![]() 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,若
,若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,求椭圆的方程.
,求椭圆的方程.
【题目】稠环芳香烃化合物中有不少是致癌物质,比如学生钟爱的快餐油炸食品中会产生苯并芘,它是由一个苯环和一个芘分子结合而成的稠环芳香烃类化合物,长期食用会致癌.下面是一组稠环芳香烃的结构简式和分子式:
名称 | 萘 | 蒽 | 并四苯 | … | 并n苯 |
结构简式 |
|
|
| … | … |
分子式 |
|
|
| … | … |
由此推断并十苯的分子式为________.