题目内容
向量 ,
, ,对任意t∈R,恒有
,对任意t∈R,恒有 ,下列四个结论中判断正确的是
,下列四个结论中判断正确的是
- A.
 ∥
∥
- B.
 ∥
∥
- C.
 ⊥
⊥
- D.
 ⊥
⊥
D
分析:利用向量模的平方等于向量的平方,得到新的不等式恒成立,利用二次不等式恒成立△≤0,再利用向量垂直的充要条件判断出 ⊥(
⊥( ).
).
解答:∵向量 ,
, ,对任意t∈R,恒有
,对任意t∈R,恒有 ,
,
∴ ,
,
∴ 对任意t恒成立,
对任意t恒成立,
∴△=4( )2-4
)2-4 2(2
2(2 -
- )≤0,
)≤0,
即( )2-2
)2-2
 +
+ ≤0,
≤0,
即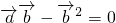 ,
,
即 ,
,
∴ ,
,
故选D.
点评:本题考查向量模的平方等于向量的平方;二次不等式恒成立的条件;向量垂直的充要条件.解题时要认真审题,仔细解答.
分析:利用向量模的平方等于向量的平方,得到新的不等式恒成立,利用二次不等式恒成立△≤0,再利用向量垂直的充要条件判断出
 ⊥(
⊥( ).
).解答:∵向量
 ,
, ,对任意t∈R,恒有
,对任意t∈R,恒有 ,
,∴
 ,
,∴
 对任意t恒成立,
对任意t恒成立,∴△=4(
 )2-4
)2-4 2(2
2(2 -
- )≤0,
)≤0,即(
 )2-2
)2-2
 +
+ ≤0,
≤0,即
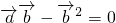 ,
,即
 ,
,∴
 ,
,故选D.
点评:本题考查向量模的平方等于向量的平方;二次不等式恒成立的条件;向量垂直的充要条件.解题时要认真审题,仔细解答.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 ,
, ,对任意t∈R,恒有
,对任意t∈R,恒有 .现给出下列四个结论:
.现给出下列四个结论: ;②
;② ;③
;③ ,④
,④
 ,
, ,对任意t∈R,恒有
,对任意t∈R,恒有 .现给出下列四个结论:
.现给出下列四个结论: ;②
;② ;③
;③ ,④
,④
 ,
, ,对任意t∈R,恒有
,对任意t∈R,恒有 ,下列四个结论中判断正确的是( )
,下列四个结论中判断正确的是( ) ∥
∥
 ∥
∥
 ⊥
⊥
 ⊥
⊥
 ,
, ,对任意t∈R,恒有
,对任意t∈R,恒有 .现给出下列四个结论:
.现给出下列四个结论: ;②
;② ;③
;③ ,④
,④
 ,
, ,对任意t∈R,恒有
,对任意t∈R,恒有 .现给出下列四个结论:
.现给出下列四个结论: ;②
;② ;③
;③ ,④
,④