题目内容
已知函数
 .
.
(1)若曲线 经过点
经过点 ,曲线
,曲线 在点
在点 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;
(2)在(1)的条件下,试求函数 (
( 为实常数,
为实常数, )的极大值与极小值之差;
)的极大值与极小值之差;
(3)若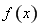 在区间
在区间 内存在两个不同的极值点,求证:
内存在两个不同的极值点,求证: .
.
【答案】
(1)
(2)当 或
或 时,
时,
 ;
;
当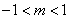 时,
时,
 ;
;
(3) .
.
【解析】
试题分析:(1)利用导数的几何意义,明确曲线 在点
在点 处的切线的斜率为
处的切线的斜率为 ,建立方程
,建立方程
 ,再根据曲线
,再根据曲线 经过点
经过点 ,得到方程
,得到方程 ,解方程组即得所求.
,解方程组即得所求.
(2)利用“表解法”,确定函数的极值,注意讨论 或
或 及
及 ,的不同情况;
,的不同情况;
(3)根据 在区间
在区间 内存在两个极值点,得到
内存在两个极值点,得到 ,
,
即 在
在 内有两个不等的实根.
内有两个不等的实根.
利用二次函数的图象和性质建立不等式组 求
求 的范围.
的范围.
试题解析:(1)
 ,
,
 直线
直线 的斜率为
的斜率为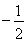 ,
, 曲线
曲线 在点
在点 处的切线的斜率为
处的切线的斜率为 ,
,
 ①
①
 曲线
曲线 经过点
经过点 ,
, ②
②
由①②得: 3分
3分
(2)由(1)知: ,
,
 ,
, , 由
, 由 ,或
,或 .
.
当 ,即
,即 或
或 时,
时, ,
, ,
, 变化如下表
变化如下表
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| | 极大值 |
| 极小值 |
|
由表可知:

 5分
5分
当 即
即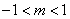 时,
时, ,
, ,
, 变化如下表
变化如下表
|
|
|
|
|
|
| - | 0 | + | 0 | - |
| | 极小值 |
| 极大值 |
|
由表可知:

 7分
7分
综上可知:当 或
或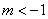 时,
时,
 ;
;
当 时,
时,
 8分
8分
(3)因为 在区间
在区间 内存在两个极值点 ,所以
内存在两个极值点 ,所以 ,
,
即 在
在 内有两个不等的实根.
内有两个不等的实根.
∴ 10分
10分
由 (1)+(3)得: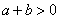 , 11分
, 11分
由(4)得: ,由(3)得:
,由(3)得: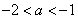 ,
,

 ,∴
,∴ .
.
故 13分
13分
考点:导数的几何意义,应用导数研究函数的单调性、极值,二次函数的图象和性质,不等式组的解法.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
















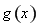

 -2lnx、
-2lnx、 -2lnx、
-2lnx、 -2lnx、
-2lnx、 -2lnx、
-2lnx、