题目内容
已知f(x)是定义在[-1,1]上的奇函数.当a、b∈[-1,1],且a+b≠0时,有(1)判断函数f(x)的单调性,并给以证明;
(2)若f(1)=1,且f(x)≤m2-2bm+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数m的取值范围.
解:(1)x1、x2∈[-1,1]且x1<x2,在![]() >0中,令a=x1,b=-x2,有
>0中,令a=x1,b=-x2,有![]() >0.
>0.
∵x1<x2,∴x1-x2<0.
又f(x)是奇函数,∴f(-x2)=-f(x2).
∴![]() >0.
>0.
故f(x1)-f(x2)<0,即f(x1)<f(x2).
∴f(x)在[-1,1]上为增函数.
(2)∵f(1)=1且f(x)在[-1,1]上为增函数,∴对x∈[-1,1],有f(x)≤f(1)=1.由题意,对所有的x∈[-1,1],b∈[-1,1],有f(x)≤m2-2bm+1恒成立,应有m2-2bm+1≥1 ![]() m2-2bm≥0.记g(b)=-2mb+m2,对所有的b∈[-1,1],g(b)≥0成立,只需
m2-2bm≥0.记g(b)=-2mb+m2,对所有的b∈[-1,1],g(b)≥0成立,只需![]() 解得m的取值范围是m∈(-∞,-2]∪{0}∪[2,+∞).
解得m的取值范围是m∈(-∞,-2]∪{0}∪[2,+∞).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 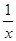 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
