题目内容
将正整数12分解成两个正整数的乘积有:1×12,2×6,3×4三种,其中3×4是这三种分解中两数差的绝对值最小的,我们称3×4为12的最佳分解,当p×q(p≤q且p、q∈N*)是正整数n的最佳分解时,我们规定函数f(n)=| p |
| q |
| 3 |
| 4 |
①f(1)=
| 1 |
| 7 |
②f(24)=
| 3 |
| 8 |
③f(28)=
| 4 |
| 7 |
④f(144)=
| 9 |
| 16 |
其中正确的序号为
分析:将各个数的分解因式写出,利用f(n)的定义求出求出各个f(n),从而判断出各命题的正误.
解答:解:对于①,因为7=1×7; 所以f(7)=
,故①对
对于②,因为24=1×24; 24=2×12; 24=3×8; 24=4×6所以f(24)=
故②错
对于③,因为28=1×28,28=2×14,28=4×7,所以f(28)=
故③对;
对于④因为144=1×144,144=2×72,144=3×48,144=12×12,144=9×16所以f(144)=1故④错.
故答案为:①③.
| 1 |
| 7 |
对于②,因为24=1×24; 24=2×12; 24=3×8; 24=4×6所以f(24)=
| 4 |
| 6 |
对于③,因为28=1×28,28=2×14,28=4×7,所以f(28)=
| 4 |
| 7 |
对于④因为144=1×144,144=2×72,144=3×48,144=12×12,144=9×16所以f(144)=1故④错.
故答案为:①③.
点评:本题考查通过题中的新定义解题,关键理解新定义.新定义题是常考的题型要重视.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
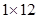 ,
, ,
,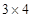 三种,其中
三种,其中 是正整数
是正整数 的最佳分解时,我们规定函数
的最佳分解时,我们规定函数 ,例如
,例如 .关于函数
.关于函数 有下列叙述: ①
有下列叙述: ① ,②
,② ,③
,③ ,④
,④ .其中正确的序号为 (填入所有正确的序号).
.其中正确的序号为 (填入所有正确的序号). ,
,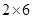 ,
, 三种,其中
三种,其中 是正整数
是正整数 的最佳分解时,我们规定函数
的最佳分解时,我们规定函数 ,例如
,例如 .
. 有下列叙述:①
有下列叙述:① ,②
,② ,③
,③ ,④
,④ .其中正确的序号为 (填入所有正确的序号).
.其中正确的序号为 (填入所有正确的序号).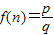 .如
.如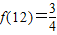 .以下有关
.以下有关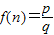 的说法中,正确的个数为( )
的说法中,正确的个数为( )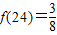 ;
;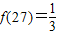 ;
;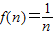 ;
;