题目内容
已知抛物线C的顶点在原点,焦点为F(2,0).
(1)求抛物线C的方程;
(2)过N(-1,0)的直线l交曲C于A,B两点,又AB的中垂线交y轴于点D(0,t),求t的取值范围.
解:(1)设抛物线方程为y2=2px,则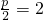 ,∴p=4,
,∴p=4,
所以,抛物线的方程是y2=8x.(4分)
(2)由题设知,直线l的斜率存在,故设直线l的方程是y=k(x+1),联立 ,消去x得ky2-8y+8k=0,(6分)
,消去x得ky2-8y+8k=0,(6分)
显然k≠0,由△=64-32k2>0,得0<|k|< .(8分)
.(8分)
由韦达定理得,y1+y2= ,y1y2=8,
,y1y2=8,
所以 ,则AB中点E坐标是(
,则AB中点E坐标是( ),(10分)
),(10分)
由kDE-k=-1可得k3t-3k2-4=0,
所以,t= ,令
,令 ,则t=4x3+3x,其中|x|
,则t=4x3+3x,其中|x| ,(12分)
,(12分)
因为t′=12x2+3>0,所以函数t=4x3+3x是在(- ),(
),(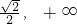 )上增函数.
)上增函数.
所以,t的取值范围是(- )∪
)∪ .(15分)
.(15分)
分析:(1)设抛物线方程为y2=2px,则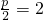 ,由此能求出抛物线的方程.
,由此能求出抛物线的方程.
(2)直线l的方程是y=k(x+1),联立 ,消去x得ky2-8y+8k=0,再由根的判别别式和韦达定理能够推导出t的取值范围
,消去x得ky2-8y+8k=0,再由根的判别别式和韦达定理能够推导出t的取值范围 .
.
点评:本题考查抛手线的性质和应用,解题时要注意根的判别式和韦达定理的合理运用.
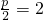 ,∴p=4,
,∴p=4,所以,抛物线的方程是y2=8x.(4分)
(2)由题设知,直线l的斜率存在,故设直线l的方程是y=k(x+1),联立
 ,消去x得ky2-8y+8k=0,(6分)
,消去x得ky2-8y+8k=0,(6分)显然k≠0,由△=64-32k2>0,得0<|k|<
 .(8分)
.(8分)由韦达定理得,y1+y2=
 ,y1y2=8,
,y1y2=8,所以
 ,则AB中点E坐标是(
,则AB中点E坐标是( ),(10分)
),(10分)由kDE-k=-1可得k3t-3k2-4=0,
所以,t=
 ,令
,令 ,则t=4x3+3x,其中|x|
,则t=4x3+3x,其中|x| ,(12分)
,(12分)因为t′=12x2+3>0,所以函数t=4x3+3x是在(-
 ),(
),(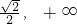 )上增函数.
)上增函数.所以,t的取值范围是(-
 )∪
)∪ .(15分)
.(15分)分析:(1)设抛物线方程为y2=2px,则
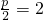 ,由此能求出抛物线的方程.
,由此能求出抛物线的方程.(2)直线l的方程是y=k(x+1),联立
 ,消去x得ky2-8y+8k=0,再由根的判别别式和韦达定理能够推导出t的取值范围
,消去x得ky2-8y+8k=0,再由根的判别别式和韦达定理能够推导出t的取值范围 .
.点评:本题考查抛手线的性质和应用,解题时要注意根的判别式和韦达定理的合理运用.

练习册系列答案
相关题目
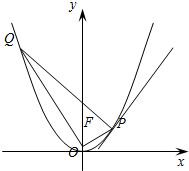 已知抛物线C的顶点在原点,焦点为F(0,1).
已知抛物线C的顶点在原点,焦点为F(0,1).