题目内容
与椭圆 有相同的焦点且过点P(2,1)的双曲线方程是________.
有相同的焦点且过点P(2,1)的双曲线方程是________.

分析:根据椭圆
 方程,得到a2=4且b2=1,所以c2=a2-b2=3,再设所求双曲线方程为
方程,得到a2=4且b2=1,所以c2=a2-b2=3,再设所求双曲线方程为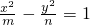 ,(m>0,n>0).然后结合题意:双曲线与椭圆
,(m>0,n>0).然后结合题意:双曲线与椭圆 有相同的焦点且过点P(2,1),列出方程组并解之可得m=2,n=1,从而得到所求双曲线的方程.
有相同的焦点且过点P(2,1),列出方程组并解之可得m=2,n=1,从而得到所求双曲线的方程.解答:∵椭圆
 中,a2=4,b2=1,
中,a2=4,b2=1,∴c2=a2-b2=3
设双曲线方程为
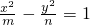 ,(m>0,n>0)
,(m>0,n>0)∵双曲线与椭圆
 有相同的焦点且过点P(2,1),
有相同的焦点且过点P(2,1),∴m+n=3且
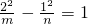 ,解之可得m=2,n=1
,解之可得m=2,n=1∴双曲线方程是
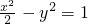 .
.故答案为:
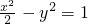
点评:本题给出与已知椭圆共焦点的双曲线且经过一个已知定点,求双曲线的标准方程,着重考查了椭圆的基本概念和双曲线的简单几何性质,属于基础题.

练习册系列答案
相关题目
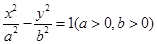 与椭圆
与椭圆 有相同的焦点
有相同的焦点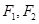 ,且该双曲线
,且该双曲线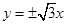 .
. 作斜率不为零的直线与此双曲线的左,右两支分别交于点
作斜率不为零的直线与此双曲线的左,右两支分别交于点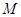 、
、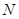 ,
,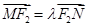 ,当
,当 轴上的点
轴上的点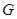 满足
满足 时,求点
时,求点 有相同的焦点且以
有相同的焦点且以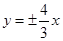 为渐近线的双曲线方程为 .
为渐近线的双曲线方程为 .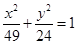 有相同的焦点且以
有相同的焦点且以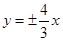 为渐近线的双曲线方程 .
为渐近线的双曲线方程 .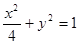 有相同的焦点且过点P
有相同的焦点且过点P 的双曲线方程是
的双曲线方程是  有相同的焦点且离心率为2的双曲线标准方程是 .
有相同的焦点且离心率为2的双曲线标准方程是 .