题目内容
已知:函数f(x)=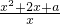 ,x∈[1,+∞],
,x∈[1,+∞],
(1)当a=-1时,判断并证明函数的单调性并求f(x)的最小值;
(2)若对任意x∈[1,+∞],f(x)>0都成立,试求实数a的取值范围.
解:(1)当a=-1时f(x)=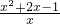 =x-
=x- +2
+2
f′(x)=1+ >0,x∈[1,+∞],所以f(x)在x∈[1,+∞]上是增函数,
>0,x∈[1,+∞],所以f(x)在x∈[1,+∞]上是增函数,
所以x=1时f(x)取最小值,最小值为2
(2)若对任意x∈[1,+∞]f(x)>0恒成立,则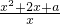 >0对任意x∈[1,+∞]恒成立,所以x2+2x+a>0对任意x∈[1,+∞]恒成立,令g(x)=x2+2x+a,x∈[1,+∞],
>0对任意x∈[1,+∞]恒成立,所以x2+2x+a>0对任意x∈[1,+∞]恒成立,令g(x)=x2+2x+a,x∈[1,+∞],
因为g(x)=x2+2x+a在∈[1,+∞],上单调递增,
所以x=1时g(x)取最小值,最小值为3+a,
∵3+a>0,∴a>-3.
分析:(1)当a=-1时f(x)=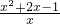 =x-
=x- +2,利用导数工具证明即可
+2,利用导数工具证明即可
(2)对任意x∈[1,+∞],f(x)>0都成立,转化为x2+2x+a>0对任意x∈[1,+∞]恒成立即可.
点评:本题考查函数单调性的判断与证明,不等式恒成立问题.考查转化、计算能力.
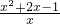 =x-
=x- +2
+2f′(x)=1+
 >0,x∈[1,+∞],所以f(x)在x∈[1,+∞]上是增函数,
>0,x∈[1,+∞],所以f(x)在x∈[1,+∞]上是增函数,所以x=1时f(x)取最小值,最小值为2
(2)若对任意x∈[1,+∞]f(x)>0恒成立,则
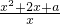 >0对任意x∈[1,+∞]恒成立,所以x2+2x+a>0对任意x∈[1,+∞]恒成立,令g(x)=x2+2x+a,x∈[1,+∞],
>0对任意x∈[1,+∞]恒成立,所以x2+2x+a>0对任意x∈[1,+∞]恒成立,令g(x)=x2+2x+a,x∈[1,+∞],因为g(x)=x2+2x+a在∈[1,+∞],上单调递增,
所以x=1时g(x)取最小值,最小值为3+a,
∵3+a>0,∴a>-3.
分析:(1)当a=-1时f(x)=
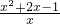 =x-
=x- +2,利用导数工具证明即可
+2,利用导数工具证明即可(2)对任意x∈[1,+∞],f(x)>0都成立,转化为x2+2x+a>0对任意x∈[1,+∞]恒成立即可.
点评:本题考查函数单调性的判断与证明,不等式恒成立问题.考查转化、计算能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目