题目内容
在某校教师趣味投篮比赛中,比赛规则是:每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖.已知教师甲投进每个球的概率都是
.
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率.
| 2 | 3 |
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率.
分析:(Ⅰ)可知X的所有可能取值为0,1,2,3,4,5,6,X~B(6,
),求概率可得分布列,可得期望;(Ⅱ)由题意可得P(A)=
(
)2(
)4+
(
)1(
)5+(
)5,计算可得.
| 2 |
| 3 |
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 1 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:(Ⅰ)由题意可得X的所有可能取值为0,1,2,3,4,5,6
由条件可知X~B(6,
),P(X=k)=
(
)k(
)6-k,(k=0,1,2,3,4,5,6)
故X的分布列为
故EX=0×
+1×
+2×
+3×
+4×
+5×
+6×
=
=4
当然若只求期望不写分布列可得EX=6×
=4;
(Ⅱ)设教师甲在一场比赛中获奖为事件A,
包含恰好投进4个球,恰好投进5个球,恰好投进6个球,
故P(A)=
(
)2(
)4+
(
)1(
)5+(
)5=
,
故教师甲在一场比赛中获奖的概率为
由条件可知X~B(6,
| 2 |
| 3 |
| C | k 6 |
| 2 |
| 3 |
| 1 |
| 3 |
故X的分布列为
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||||||
| P |
|
|
|
|
|
|
|
| 1 |
| 729 |
| 12 |
| 729 |
| 60 |
| 729 |
| 160 |
| 729 |
| 240 |
| 729 |
| 192 |
| 729 |
| 64 |
| 729 |
| 2916 |
| 729 |
当然若只求期望不写分布列可得EX=6×
| 2 |
| 3 |
(Ⅱ)设教师甲在一场比赛中获奖为事件A,
包含恰好投进4个球,恰好投进5个球,恰好投进6个球,
故P(A)=
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 1 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 32 |
| 81 |
故教师甲在一场比赛中获奖的概率为
| 32 |
| 81 |
点评:本题考查离散型随机变量的分布列即期望,以及独立重复试验的概率,属中档题.

练习册系列答案
相关题目
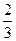 .
. Ⅰ)记教师甲在每场
Ⅰ)记教师甲在每场 的6次投球中投进球的个数为X,求X的分布列及数学期望;
的6次投球中投进球的个数为X,求X的分布列及数学期望; 赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗? 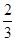 .
.