题目内容
(本小题12分) 如图,在五面体 中,
中, ∥
∥ ,
, ,
, ,四边形
,四边形 为平行四边形,
为平行四边形, 平面
平面 ,
, .
.
求:(1)直线 到平面
到平面 的距离;
的距离;
(2)二面角 的平面角的正切值.
的平面角的正切值.

(1) ;(2)
;(2) .
.
【解析】第一问中利用三垂线定理得到。第二问运用二面角的定义作出角或者利用空间向量法表示法向量从而得到二面角的平面角的大小。
第一问(1)AB∥DCDC 平面EFCD,
平面EFCD,  AB到面EFCD,的距离等于点A到面EFCD,的距离,过点A作
AB到面EFCD,的距离等于点A到面EFCD,的距离,过点A作 于G,因
于G,因 AB∥DC,故CD
AB∥DC,故CD AD;又
AD;又 FA
FA 平面ABCD,由三垂线定理可知,CD
平面ABCD,由三垂线定理可知,CD FD,故CD
FD,故CD FAD,知CD
FAD,知CD AG,所以AG为所求直线AB到面EFCD,的距离
AG,所以AG为所求直线AB到面EFCD,的距离
在 中,
中,
由 平面ABCD,得FA
平面ABCD,得FA AD,从而在
AD,从而在 中,
中,

 。即直线AB到平面EFCD,的距离为
。即直线AB到平面EFCD,的距离为 。
。
(2)中由己知,FA 平面ABCD,得FA
平面ABCD,得FA AD,又由
AD,又由 ,知DA
,知DA AB,故AD
AB,故AD 平面ABFE
平面ABFE
 DA
DA AE,所以,
AE,所以, 为二面角F-AD-E的平面角,记为
为二面角F-AD-E的平面角,记为 .
.
在 中, AE=
中, AE= ,由ABCD得,FE//AB,从而
,由ABCD得,FE//AB,从而
在 中, FE=
中, FE= ,故
,故
所以二面角 的平面角的正切值为
的平面角的正切值为 .
.
解:(1)AB∥DCDC 平面EFCD,
平面EFCD,  AB到面EFCD,的距离等于点A到面EFCD,的距离,过点A作
AB到面EFCD,的距离等于点A到面EFCD,的距离,过点A作 于G,因
于G,因 AB∥DC,故CD
AB∥DC,故CD AD;又
AD;又 FA
FA 平面ABCD,由三垂线定理可知,CD
平面ABCD,由三垂线定理可知,CD FD,故CD
FD,故CD FAD,知CD
FAD,知CD AG,所以AG为所求直线AB到面EFCD,的距离
AG,所以AG为所求直线AB到面EFCD,的距离
在 中,
中,
由 平面ABCD,得FA
平面ABCD,得FA AD,从而在
AD,从而在 中,
中,

 。即直线AB到平面EFCD,的距离为
。即直线AB到平面EFCD,的距离为 。
。
(2)由己知,FA 平面ABCD,得FA
平面ABCD,得FA AD,又由
AD,又由 ,知DA
,知DA AB,故AD
AB,故AD 平面ABFE
平面ABFE
 DA
DA AE,所以,
AE,所以, 为二面角F-AD-E的平面角,记为
为二面角F-AD-E的平面角,记为 .
.
在 中,
中,  ,由ABCD得,
,由ABCD得, ,从而
,从而
在 中,
中,  ,故
,故
所以二面角 的平面角的正切值为
的平面角的正切值为 .
.
解法二:
(1)如图以A点为坐标原点, 的方向为
的方向为 的正方向建立空间直角坐标系数,则
的正方向建立空间直角坐标系数,则

A(0,0,0) C(2,2,0) D(0,2,0) 设 可得
可得 ,由
,由 .即
.即 ,解得
,解得

 ∥
∥ ,
,
 面
面 ,所以直线AB到面
,所以直线AB到面 的距离等于点A到面
的距离等于点A到面 的距离。设A点在平面
的距离。设A点在平面 上的射影点为
上的射影点为 ,则
,则 因
因 且
且 ,而
,而
 ,此即
,此即 解得
解得 ① ,知G点在
① ,知G点在 面上,故G点在FD上.
面上,故G点在FD上.
 ,
, 故有
故有 ② 联立①,②解得,
② 联立①,②解得,  [
[

 为直线AB到面
为直线AB到面 的距离. 而
的距离. 而 所以
所以
(2)因四边形 为平行四边形,则可设
为平行四边形,则可设 ,
, .由
.由
 得
得 ,解得
,解得 .即
.即 .故
.故
由 ,
, 因
因 ,
, ,故
,故 为二面角
为二面角 的平面角,又
的平面角,又
 ,
, ,
, ,所以
,所以

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
 是以原点
是以原点 为中心,以
为中心,以 、
、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以
是以 是曲线
是曲线 为钝角,若
为钝角,若 ,
, .
. 、
、 、
、 、
、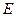 四点(如图),若
四点(如图),若 为
为 的中点,
的中点, 为
为 的中点,问
的中点,问 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由. <
< <
< <…<
<…< )是曲线C
)是曲线C
 上的n个点,点
上的n个点,点 在x轴的正半轴上,且⊿
在x轴的正半轴上,且⊿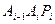 是正三角形(
是正三角形( 是坐标原点)。
是坐标原点)。

 的横坐标
的横坐标 关于n的表达式并用数学归纳法证明
关于n的表达式并用数学归纳法证明 中,
中,
 ,
, 为
为 中点,若规定主视方向为垂直于平面
中点,若规定主视方向为垂直于平面 的方向,则可求得三棱柱左视图的面积为
的方向,则可求得三棱柱左视图的面积为 ;
;
 ;
; 的体积。
的体积。 海里的两个观测点。现位于B点正北方向、A点北偏东
海里的两个观测点。现位于B点正北方向、A点北偏东 方向的C点有一艘轮船发出求救信号,位于B点北偏西
方向的C点有一艘轮船发出求救信号,位于B点北偏西 、A点北偏西
、A点北偏西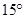 的D点的救援船立即前往营救,其航行速度为
的D点的救援船立即前往营救,其航行速度为 海里/小时.问该救援船到达C点需要多少时间?
海里/小时.问该救援船到达C点需要多少时间?
 的算法的
的算法的