题目内容
在△ABC中，若a=2，tanA•sin2B=tanB•sin2A，A=30°，则B等于________．
60°或30°
分析：把已知等式的左边利用同角三角函数间的基本关系切化弦，右边利用正弦定理变形，然后根据二倍角的正弦函数公式化简，由A和B为三角形的内角，根据正弦函数图象与性质得到A与B角度之间的关系，
解答：由正弦定理得：
=
=2R，（R为三角形外接圆的半径）
∴a=2RsinA，b=2RsinB，
∴tanA•sin2B=tanB•sin2A，变形为：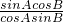
=
，
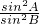化简得：2sinBcosB=2sinAcosA，即sin2B=sin2A，
∴2A=2B或2A=π-2B?A=B或A+B=
∵A=30°
∴B=30°或60°
故答案：30°或60°
点评：此题考查了正弦定理，三角函数的恒等变换及正弦函数图象与性质．根据正弦定理及同角三角函数公式化简已知的等式是本题的突破点．
分析：把已知等式的左边利用同角三角函数间的基本关系切化弦，右边利用正弦定理变形，然后根据二倍角的正弦函数公式化简，由A和B为三角形的内角，根据正弦函数图象与性质得到A与B角度之间的关系，
解答：由正弦定理得：
==2R，（R为三角形外接圆的半径）∴a=2RsinA，b=2RsinB，
∴tanA•sin2B=tanB•sin2A，变形为：
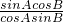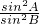=，化简得：2sinBcosB=2sinAcosA，即sin2B=sin2A，
∴2A=2B或2A=π-2B?A=B或A+B=
∵A=30°
∴B=30°或60°
故答案：30°或60°
点评：此题考查了正弦定理，三角函数的恒等变换及正弦函数图象与性质．根据正弦定理及同角三角函数公式化简已知的等式是本题的突破点．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
在△ABC中，若a=7，b=3，c=8，则其面积等于（ ）
| A、12 | ||
B、
| ||
| C、28 | ||
D、6
|