Question

已知椭圆的顶点与双曲线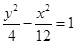的焦点重合，它们的离心率之和为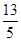，若椭圆的焦点在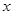轴上，求椭圆的方程.

 

Answer 1

【答案】

【解析】

试题分析：设所求椭圆方程为，其离心率为，焦距为2，双曲线的焦距为2，离心率为，，则有：

，＝4

∴ 

∴，即 ①    

又＝4   ②

 ③

由①、 ②、③可得

∴ 所求椭圆方程为  

考点：椭圆的标准方程；椭圆的性质；双曲线的性质。

点评：本题主要考查椭圆与双曲线的简单性质，我们要注意椭圆中的关系式与双曲线中的关系式的区别。属于基础题型。