题目内容
设函数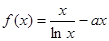 .
.
(1)若函数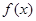 在
在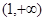 上为减函数,求实数
上为减函数,求实数 的最小值;
的最小值;
(2)若存在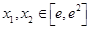 ,使
,使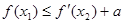 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1)a的最小值为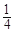 ;(2)
;(2)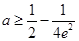 .
.
解析试题分析:(1)根据f (x)在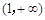 上为减函数,得到
上为减函数,得到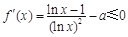 在
在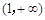 上恒成立.转化成
上恒成立.转化成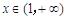 时,
时,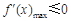 .
.
应用导数确定其最大值为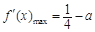 .
.
(2)应用“转化与化归思想”,对命题进行一系列的转化,“若存在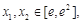 使
使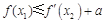 成立”等价于“当
成立”等价于“当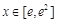 时,有
时,有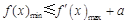 ”.
”.
由(1)问题等价于:“当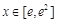 时,有
时,有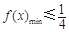 ”.
”.
讨论①当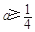 时,②当
时,②当 <
<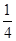 时,
时, ,作出结论.
,作出结论.
(1)由已知得x>0,x≠1.
因f (x)在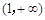 上为减函数,故
上为减函数,故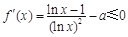 在
在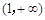 上恒成立. 1分
上恒成立. 1分
所以当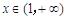 时,
时,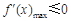 .
.
又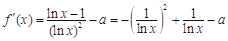
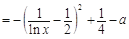 , 2分
, 2分
故当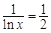 ,即
,即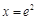 时,
时,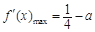 .
.
所以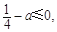 于是
于是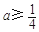 ,故a的最小值为
,故a的最小值为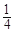 . 4分
. 4分
(2)命题“若存在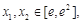 使
使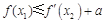 成立”等价于
成立”等价于
“当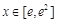 时,有
时,有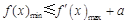 ”. 5分
”. 5分
由(1),当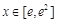 时,
时,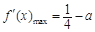 ,
,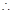
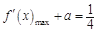 .
.
问题等价于:“当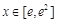 时,有
时,有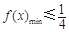 ”. 6分
”. 6分
①当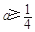 时,由(1),
时,由(1),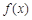 在
在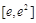 上为减函数,
上为减函数,
则 =
=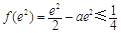 ,故
,故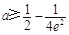 . 8分
. 8分
②当 <
<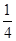 时,由于
时,由于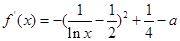 在
在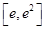 上的值域为
上的值域为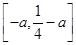
(ⅰ)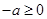 ,即
,即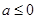 ,
,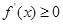 在
在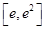 恒成立,故
恒成立,故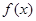 在
在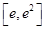 上为增函数,
上为增函数,
于是,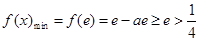 ,矛盾. 10分
,矛盾. 10分
(ⅱ)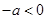 ,即
,即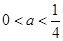 ,由
,由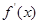 的单调性和值域知,
的单调性和值域知,
存在唯一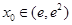 ,使
,使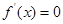 ,且满足:
,且满足:
当
练习册系列答案
相关题目
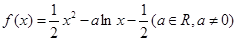 .
.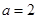 时,求曲线
时,求曲线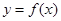 在点
在点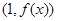 处的切线方程;
处的切线方程;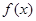 的单调区间;
的单调区间; 都有
都有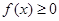 恒成立,求实数
恒成立,求实数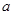 的取值范围.
的取值范围.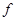 (
( ) =
) =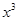 ,g (
,g (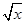 。
。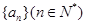 满足
满足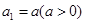 ,
,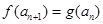 ,证明:存在常数M,使得对于任意的
,证明:存在常数M,使得对于任意的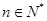 ,都有
,都有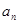 ≤
≤ 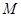 .
.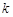
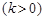 .现已知相距18
.现已知相距18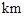 的A,B两家化工厂(污染源)的污染强度分别为
的A,B两家化工厂(污染源)的污染强度分别为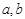 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数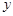 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设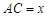 (
(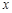 的函数; (2)若
的函数; (2)若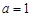 ,且
,且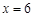 时,
时,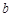 的值.
的值.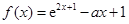 ,
, .
. 在点
在点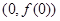 处的切线与直线
处的切线与直线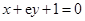 垂直,求
垂直,求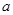 的值;
的值;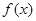 的单调区间;
的单调区间; ,当
,当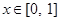 时,都有
时,都有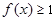 成立,求实数
成立,求实数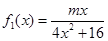 ,
,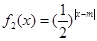 ,其中m∈R.
,其中m∈R.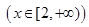 的单调性,并证明你的结论;
的单调性,并证明你的结论;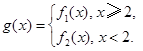 若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.
若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围. 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.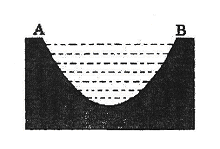
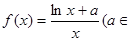 R).
R).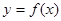 在点
在点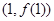 处的切线与直线
处的切线与直线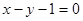 平行,求
平行,求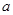 的值;
的值; 的单调区间和极值;
的单调区间和极值;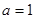 ,且
,且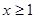 时,证明:
时,证明: