题目内容
【题目】如图,椭圆M: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,直线x=±a和y=±b所围成的矩形ABCD的面积为8.
,直线x=±a和y=±b所围成的矩形ABCD的面积为8.
(Ⅰ)求椭圆M的标准方程;
(Ⅱ)设直线l:y=x+m(m∈R)与椭圆M有两个不同的交点P,Q,l与矩形ABCD有两个不同的交点S,T.求 ![]() 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.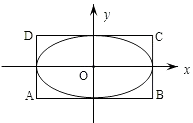
【答案】解:(I) ![]() …①
…①
矩形ABCD面积为8,即2a2b=8…②
由①②解得:a=2,b=1,
∴椭圆M的标准方程是 ![]() .
.
(II) 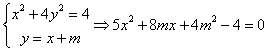 ,
,
由△=64m2﹣20(4m2﹣4)>0得 ![]() .
.
设P(x1 , y1),Q(x2 , y2),则 ![]() ,
,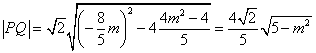 .
.
当l过A点时,m=1,当l过C点时,m=﹣1.
①当 ![]() 时,有
时,有 ![]() ,
, 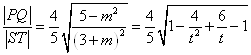 ,
,
其中t=m+3,由此知当 ![]() ,即
,即 ![]() 时,
时, ![]() 取得最大值
取得最大值 ![]() .
.
②由对称性,可知若 ![]() ,则当
,则当 ![]() 时,
时, ![]() 取得最大值
取得最大值 ![]() .
.
③当﹣1≤m≤1时, ![]() ,
, ![]() ,
,
由此知,当m=0时, ![]() 取得最大值
取得最大值 ![]() .
.
综上可知,当 ![]() 或m=0时,
或m=0时, ![]() 取得最大值
取得最大值 ![]()
【解析】(Ⅰ)通过椭圆的离心率,矩形的面积公式,直接求出a,b,然后求椭圆M的标准方程;(Ⅱ) 通过 ![]()
![]() 时,求出
时,求出 ![]() 取得最大值
取得最大值 ![]() .利用由对称性,推出
.利用由对称性,推出 ![]() ,
, ![]() 取得最大值
取得最大值 ![]() .③当﹣1≤m≤1时,
.③当﹣1≤m≤1时, ![]() 取得最大值
取得最大值 ![]() .求
.求 ![]() 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
【考点精析】关于本题考查的椭圆的标准方程,需要了解椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.

练习册系列答案
相关题目