题目内容
四棱锥P—ABCD中,底面ABCD是一个平行四边形,(1)求证PA⊥底面ABCD;
(2)求四棱锥P—ABCD的体积;
(3)对于向量a=(x1,y1,z1),b=(x2,y2,z2),c=(x3,y3,z3),定义一种运算:
(a×b)·c=x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2y1z3-x3y2z1.
试计算(![]() ×
×![]() )·
)·![]() 的绝对值的值;说明其与四棱锥P—ABCD体积的关系,并由此猜想向量这一运算(
的绝对值的值;说明其与四棱锥P—ABCD体积的关系,并由此猜想向量这一运算(![]() ×
×![]() )·
)·![]() 的绝对值的几何意义.
的绝对值的几何意义.
解析:(1)∵![]() ·
·![]() =-2-2+4=0,
=-2-2+4=0,
∴AP⊥AB.
又∵![]() ·
·![]() =-4+4+0=0,
=-4+4+0=0,
∴AP⊥AD,∵AB、AD是底面ABCD上的两条相交直线,∴AP⊥底面ABCD.
(2)设![]() 与
与![]() 的夹角为θ,则
的夹角为θ,则
cosθ=
=![]() .
.
V=![]() |
|![]() |·|
|·|![]() |·sinθ·|
|·sinθ·|![]() |=
|=![]()
![]() ·
·![]() ·
·![]() =16.
=16.
(3)|(![]() ×
×![]() )·
)·![]() |=|-4-32-4-8|它是四棱锥P—ABCD体积的3倍.
|=|-4-32-4-8|它是四棱锥P—ABCD体积的3倍.
猜测:|(![]() ×
×![]() )·
)·![]() |在几何上可表示以AB、AD、AP为棱的平行六面体的体积(或以AB、AD、AP为棱的直四棱柱的体积).
|在几何上可表示以AB、AD、AP为棱的平行六面体的体积(或以AB、AD、AP为棱的直四棱柱的体积).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
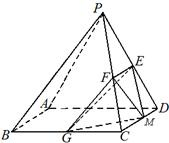 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.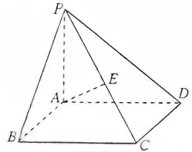 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2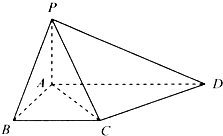 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.