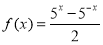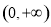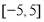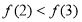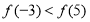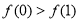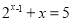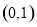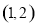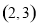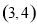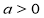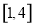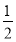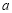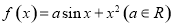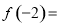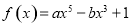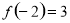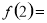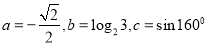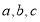题目内容
已知点 ,
, 是函数
是函数
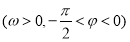 图象上的任意两点,且角
图象上的任意两点,且角 的终边经过点
的终边经过点 ,若
,若 时,
时, 的最小值为
的最小值为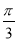 .
.
(1)求函数 的解析式;
的解析式;
(2)求函数 的单调递增区间;
的单调递增区间;
(3)当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)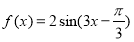 ;(2)
;(2)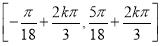
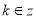 ;(3)
;(3)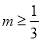 .
.
【解析】
试题分析:(1)有三角函数定义得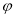 值,
值, 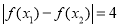 ,
,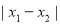 的最小值为
的最小值为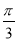 ,可知
,可知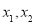 是相邻的两个对称轴,从而得周期;(2)利用整体思想
是相邻的两个对称轴,从而得周期;(2)利用整体思想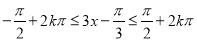 ;(3)由
;(3)由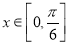 利用整体思想求出
利用整体思想求出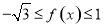 ,不等式
,不等式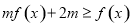 恒成立问题,因为
恒成立问题,因为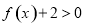 ,所以可以把
,所以可以把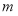 分离出来,
分离出来,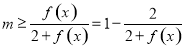 求得.
求得.
试题解析:【解析】
(1)角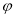 的终边经过点
的终边经过点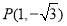 ,
,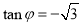 , 2分
, 2分
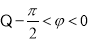 ,
,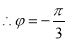 . 3分
. 3分
由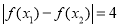 时,
时,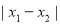 的最小值为
的最小值为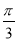 ,
,
得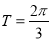 ,即
,即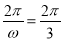 ,
,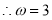 ..5分
..5分
∴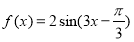 6分
6分
(2)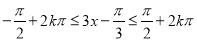 ,即
,即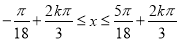 , 8分
, 8分
 函数
函数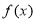 的单调递增区间为
的单调递增区间为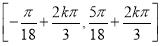
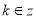 9分
9分
(3) 当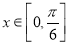 时,
时,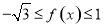 , 11分
, 11分
于是,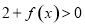 ,
,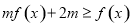
等价于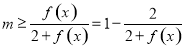 12分
12分
由 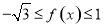 , 得
, 得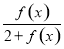 的最大值为
的最大值为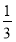 13分
13分
所以,实数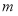 的取值范围是
的取值范围是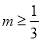 。 14分
。 14分
注:用别的方法求得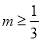 ,只要正确就给3分。
,只要正确就给3分。
考点:1.三角函数定义;2.三角函数的性质;3.恒成立问题.

练习册系列答案
相关题目