题目内容
已知点(x,y)在椭圆C: (a>b>0)的第一象限上运动.
(a>b>0)的第一象限上运动.(Ⅰ)求点
 的轨迹C1的方程;
的轨迹C1的方程;(Ⅱ)若把轨迹C1的方程表达式记为y=f(x),且在
 内y=f(x)有最大值,试求椭圆C的离心率的取值范围.
内y=f(x)有最大值,试求椭圆C的离心率的取值范围.
【答案】分析:(I)欲求点 的轨迹C1的方程,设
的轨迹C1的方程,设 ,只须求出x,y的关系式即可,利用点(x,y)在椭圆C:
,只须求出x,y的关系式即可,利用点(x,y)在椭圆C: (a>b>0)的第一象限上运动,点的坐标适合方程,即可得到x,y的关系式;
(a>b>0)的第一象限上运动,点的坐标适合方程,即可得到x,y的关系式;
(II)由轨迹C1方程是 (x>0,y>0),得
(x>0,y>0),得 (x>0).利用基本不等式求出f(x)的最大值,及取得最大值的条件得出关于a,c的不等关系,即可求得椭圆C的离心率的取值范围.
(x>0).利用基本不等式求出f(x)的最大值,及取得最大值的条件得出关于a,c的不等关系,即可求得椭圆C的离心率的取值范围.
解答:解:(Ⅰ)设点(x,y)是轨迹C1上的动点,∴ (2分)
(2分)
∴xy=y2, .
.
∵点(x,y)在椭圆C: (a>b>0)的第一象限上运动,则x>0,y>0.
(a>b>0)的第一象限上运动,则x>0,y>0.
∴ .
.
故所求的轨迹C1方程是 (x>0,y>0).(6分)
(x>0,y>0).(6分)
(Ⅱ)由轨迹C1方程是 (x>0,y>0),得
(x>0,y>0),得 (x>0).
(x>0).
∴ ≤
≤ .
.
所以,当且仅当 ,即
,即 时,f(x)有最大值.(10分)
时,f(x)有最大值.(10分)
如果在开区间 内y=f(x)有最大值,只有
内y=f(x)有最大值,只有 .(12分)
.(12分)
此时, ,解得
,解得 .
.
∴椭圆C的离心率的取值范围是 .(14分)
.(14分)
点评:本小题主要考查椭圆的简单性质、轨迹方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
 的轨迹C1的方程,设
的轨迹C1的方程,设 ,只须求出x,y的关系式即可,利用点(x,y)在椭圆C:
,只须求出x,y的关系式即可,利用点(x,y)在椭圆C: (a>b>0)的第一象限上运动,点的坐标适合方程,即可得到x,y的关系式;
(a>b>0)的第一象限上运动,点的坐标适合方程,即可得到x,y的关系式;(II)由轨迹C1方程是
 (x>0,y>0),得
(x>0,y>0),得 (x>0).利用基本不等式求出f(x)的最大值,及取得最大值的条件得出关于a,c的不等关系,即可求得椭圆C的离心率的取值范围.
(x>0).利用基本不等式求出f(x)的最大值,及取得最大值的条件得出关于a,c的不等关系,即可求得椭圆C的离心率的取值范围.解答:解:(Ⅰ)设点(x,y)是轨迹C1上的动点,∴
 (2分)
(2分)∴xy=y2,
 .
.∵点(x,y)在椭圆C:
 (a>b>0)的第一象限上运动,则x>0,y>0.
(a>b>0)的第一象限上运动,则x>0,y>0.∴
 .
.故所求的轨迹C1方程是
 (x>0,y>0).(6分)
(x>0,y>0).(6分)(Ⅱ)由轨迹C1方程是
 (x>0,y>0),得
(x>0,y>0),得 (x>0).
(x>0).∴
 ≤
≤ .
.所以,当且仅当
 ,即
,即 时,f(x)有最大值.(10分)
时,f(x)有最大值.(10分)如果在开区间
 内y=f(x)有最大值,只有
内y=f(x)有最大值,只有 .(12分)
.(12分)此时,
 ,解得
,解得 .
.∴椭圆C的离心率的取值范围是
 .(14分)
.(14分)点评:本小题主要考查椭圆的简单性质、轨迹方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目


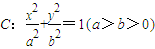 过点
过点 ,离心率
,离心率 ,若点M(x,y)在椭圆C上,则点
,若点M(x,y)在椭圆C上,则点 称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.
称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O. 过点
过点 ,离心率
,离心率 ,若点M(x,y)在椭圆C上,则点
,若点M(x,y)在椭圆C上,则点 称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.
称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O. 过点
过点 ,离心率
,离心率 ,若点M(x,y)在椭圆C上,则点
,若点M(x,y)在椭圆C上,则点 称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.
称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.