题目内容
(1)已知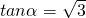 ,求cosα-sinα的值;
,求cosα-sinα的值;
(2)当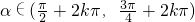 ,k∈Z时,利用三角函数线表示出sinα,cosα,tanα并比较其大小.
,k∈Z时,利用三角函数线表示出sinα,cosα,tanα并比较其大小.
解:(1)∵tanα= =
= ,可得α为第一象限角或第三象限角,…1分
,可得α为第一象限角或第三象限角,…1分
由 …2分
…2分
得:cos2α= ,sin2α=
,sin2α= …4分
…4分
①当α为第一象限角时,cosα= ,sinα=
,sinα= ,
,
故cosα-sinα=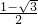 …5分
…5分
②当α为第三象限角时,cosα=- ,sinα=-
,sinα=- ,
,
故cosα-sinα=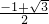 …6分
…6分
(2)如下图所示

sinα,cosα,tanα分别用有向线段MP,OM,AT表示…10分
由三角函数线知sinα>cosα>tanα…12分
分析:(1)由 可求得cos2α与sin2α,据α在第一象限角或第三象限角分类讨论,即可求得cosα-sinα的值;
可求得cos2α与sin2α,据α在第一象限角或第三象限角分类讨论,即可求得cosα-sinα的值;
(2)依题意,作出三角函数线表示出sinα,cosα,tanα,即可比较其大小.
点评:本题考查同角三角函数间的基本关系,突出分类讨论思想与方程思想的考查,考查三角函数线,考查作图能力,属于中档题.
 =
= ,可得α为第一象限角或第三象限角,…1分
,可得α为第一象限角或第三象限角,…1分由
 …2分
…2分得:cos2α=
 ,sin2α=
,sin2α= …4分
…4分①当α为第一象限角时,cosα=
 ,sinα=
,sinα= ,
,故cosα-sinα=
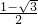 …5分
…5分②当α为第三象限角时,cosα=-
 ,sinα=-
,sinα=- ,
,故cosα-sinα=
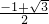 …6分
…6分(2)如下图所示

sinα,cosα,tanα分别用有向线段MP,OM,AT表示…10分
由三角函数线知sinα>cosα>tanα…12分
分析:(1)由
 可求得cos2α与sin2α,据α在第一象限角或第三象限角分类讨论,即可求得cosα-sinα的值;
可求得cos2α与sin2α,据α在第一象限角或第三象限角分类讨论,即可求得cosα-sinα的值;(2)依题意,作出三角函数线表示出sinα,cosα,tanα,即可比较其大小.
点评:本题考查同角三角函数间的基本关系,突出分类讨论思想与方程思想的考查,考查三角函数线,考查作图能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
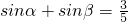
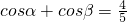 求cos(α-β)的值
求cos(α-β)的值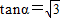 ,求cosα-sinα的值;
,求cosα-sinα的值; ,k∈Z时,利用三角函数线表示出sinα,cosα,tanα并比较其大小.
,k∈Z时,利用三角函数线表示出sinα,cosα,tanα并比较其大小.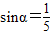 ,求cosα,tanα的值.
,求cosα,tanα的值.