方程lnx+2x=6的解一定位于区间( )A．.(1.2)B．(2.3)C．.(3.4)D．(4.5) 题目和参考答案——青夏教育精英家教网—

题目内容

19．方程lnx+2x=6的解一定位于区间（　　）

A．

.（1，2）

B．

（2，3）

C．

.（3，4）

D．

（4，5）

分析方程lnx+2x=6的根即函数f（x）=lnx+2x-6的零点，而函数f（x）=lnx+2x-6在定义域上单调连续；从而求零点的区间即可．

解答解：方程lnx+2x=6的根即函数f（x）=lnx+2x-6的零点，
函数f（x）=lnx+2x-6在定义域上单调连续；
且f（2）=ln2+4-6＜0；
f（3）=ln3+6-6＞0；
故方程lnx+2x=6的根属于区间（2，3）
故选B．

点评本题考查了方程的根与函数的零点的应用，属于基础题．

练习册系列答案

10．

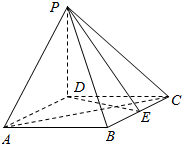如图，四棱锥P-ABCD的底面ABCD为菱形，PD⊥底面ABCD，AD=2，∠DAB=60°，E为BC的中点．
（Ⅰ）证明：AD⊥平面PDE；
（Ⅱ）若PD=2，求点E到平面PAC的距离．

7．已知函数$f（x）=（{{{log}_2}\frac{x}{2}}）•（{{{log}_{0.5}}\frac{4}{x}}）$，$（x∈[\sqrt{2}，16]）$，求：
（1）求log₂x的取值范围；
（2）求f（x）的值域．

14．三棱柱ABC-A₁B₁C₁的底是边长为1的正三角形，高AA₁=1，在AB上取一点P，设△PA₁C₁与面A₁B₁C₁所成的二面角为α，△PB₁C₁与面A₁B₁C₁所成的二面角为β，则tan（α+β）的最小值是-$\frac{8\sqrt{3}}{13}$．

4．点P在直线l：x-y-1=0上运动，A（4，1），B（2，0），则|PA|+|PB|的最小值是（　　）

11．

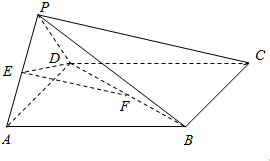如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，侧面PAD⊥底面ABCD，E，F分别为PA，BD的中点，PA=PD=AD=2，$AB=2\sqrt{2}$，∠DAB=45°．
（Ⅰ）求证：EF∥平面PBC；
（Ⅱ）求证：平面DEF⊥平面PAD．

8．已知函数f（x）是定义在（0，+∞）上的增函数，且满足：x＞0，都有f（f（x）-log₃x）=4成立，则f（9）=5．

9．

在空间四边形ABCD中，AC⊥BD，M、N分别是AB、CD的中点，AC=4，BD=3，求：MN和BD所成的角的正切值．

试题分类